Tendencia Central Y Dispersión Media Moda Y Mediana

¡Hola amigos y amigas! ¿Cómo están todos hoy? Hoy quiero hablarles de un tema muy interesante y valioso en el mundo de las matemáticas: las medidas de tendencia central y dispersión.

Medidas de posición

La primera cosa que necesitamos entender es qué son las medidas de posición. En esencia, estas son números que nos dan información relevante sobre la posición de un conjunto de datos en relación a los demás. Se utilizan para describir la distribución de los datos y pueden ser muy útiles para entender cómo se comporta cierto conjunto de datos. Los tres tipos más comunes de medidas de posición son:

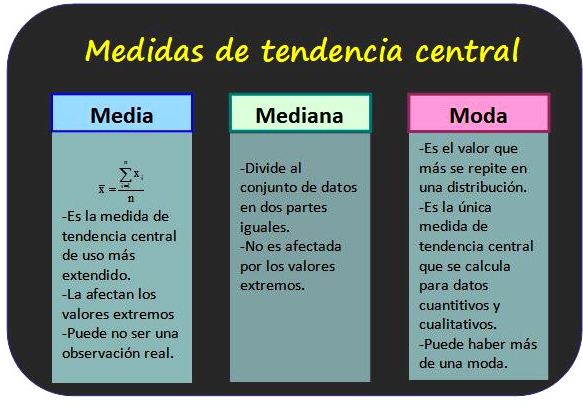
Media

La media es la medida más común que utilizamos para representar un conjunto de datos en un solo número. Para encontrar la media, sumamos todos los valores de nuestro conjunto de datos y dividimos la suma entre el número de elementos en el conjunto. Por ejemplo, si tenemos los siguientes números:

4, 5, 6, 7, 8

La suma total de estos números es 30. Dividimos 30 por 5 porque hay 5 números en el conjunto. La media de estos números es 6.

La media es muy útil porque nos da una idea de cuál es el valor "promedio" en un conjunto de datos. Sin embargo, es importante tener en cuenta que la media puede ser influenciada por valores extremos que distorsionan el resultado.

Mediana

La mediana es el valor que ocupa el lugar intermedio de un conjunto de datos ordenados. Para encontrar la mediana, debemos ordenar los números y encontrar el número que ocupa el lugar intermedio. Si el conjunto de datos tiene un número par de elementos, se toma el promedio de los dos números que quedan en el medio. Por ejemplo, si tenemos los siguientes números:

4, 5, 6, 7, 8

La mediana de estos números es 6, porque es el valor que ocupa el lugar intermedio en el conjunto de datos. Si tuviéramos los siguientes números:

4, 5, 6, 7, 8, 9

La mediana sería 6.5, porque se toma el promedio de los dos números que quedan en el medio (6 y 7).

La mediana es muy útil porque no se ve influenciada por valores extremos en el conjunto de datos. Esto significa que, en algunos casos, puede ser una medida más adecuada que la media.

Moda

La moda es el valor que aparece con más frecuencia en un conjunto de datos. Para encontrar la moda, simplemente contamos cuántas veces aparece cada número en el conjunto de datos y elegimos el que aparece con mayor frecuencia. Por ejemplo, si tenemos los siguientes números:

4, 5, 6, 6, 7, 8, 8

El número 6 y el número 8 aparecen dos veces cada uno, mientras que los demás números aparecen una vez. Por lo tanto, la moda de estos números es 6 y 8.

La moda es útil porque nos da una idea de cuál es el valor "más común" en un conjunto de datos. Sin embargo, puede haber más de una moda o puede que no haya ninguna en un conjunto de datos.

Medidas de dispersión

Una vez que entendemos las medidas de posición, podemos pasar a las medidas de dispersión, también conocidas como medidas de variabilidad. Estas medidas nos dan información sobre cómo se distribuyen los datos alrededor de las medidas de posición. Los tres tipos más comunes de medidas de dispersión son:

Desviación estándar

La desviación estándar es una medida de cuánto varían los valores en un conjunto de datos. Es una medida más precisa que el rango, porque toma en cuenta todos los valores en el conjunto de datos, no solo los valores extremos. La desviación estándar nos dice cuánto un número promedio (la media) puede variar de un valor dado en el conjunto de datos.

Para calcular la desviación estándar, necesitamos primero encontrar la media del conjunto de datos. Luego, para cada valor en el conjunto de datos, restamos la media y elevamos al cuadrado el resultado. Sumamos todos estos valores y los dividimos entre el número total de elementos en el conjunto de datos. Finalmente, sacamos la raíz cuadrada de ese número. Por ejemplo, si tenemos los siguientes números:

4, 5, 6, 7, 8

Primero encontramos la media, que es 6. Luego, para cada valor en el conjunto de datos, hacemos lo siguiente:

(4 - 6)^2 = 4

(5 - 6)^2 = 1

(6 - 6)^2 = 0

(7 - 6)^2 = 1

(8 - 6)^2 = 4

Ahora sumamos estos valores:

4 + 1 + 0 + 1 + 4 = 10

Dividimos entre el número total de elementos, que es 5:

10 / 5 = 2

Finalmente, sacamos la raíz cuadrada de 2:

√2 = 1.41

La desviación estándar de estos números es 1.41.

Rango intercuartílico

El rango intercuartílico nos dice cuánto varían los valores del conjunto de datos que se encuentran dentro del rango del 50% central de los datos ordenados. Para encontrar el rango intercuartílico, primero ordenamos los valores en el conjunto de datos. Luego, encontramos la mediana de los valores que se encuentran debajo de la mediana general (el primer cuartil) y la mediana de los valores que se encuentran por encima de la mediana general (el tercer cuartil). Restamos el primer cuartil del tercer cuartil para obtener el rango intercuartílico. Por ejemplo, si tenemos los siguientes números:

4, 5, 6, 7, 8

Primero ordenamos los números:

4, 5, 6, 7, 8

La mediana general es 6, así que encontramos la mediana de los valores debajo de 6 y la mediana de los valores por encima de 6:

Primer cuartil: 5

Tercer cuartil: 7

Restamos el primer cuartil del tercer cuartil:

7 - 5 = 2

El rango intercuartílico de estos números es 2.

Varianza

La varianza es una medida de cuánto varían los valores en un conjunto de datos. Es similar a la desviación estándar, pero es el resultado de elevar al cuadrado la desviación estándar. Para encontrar la varianza, necesitamos calcular la desviación estándar y luego elevarla al cuadrado. Por ejemplo, si tenemos los siguientes números:

4, 5, 6, 7, 8

Ya encontramos la desviación estándar de estos números, que es 1.41. Para encontrar la varianza, elevamos al cuadrado la desviación estándar:

1.41^2 = 2

La varianza de estos números es 2.

Consejos y recomendaciones

Es importante tener en cuenta que las medidas de tendencia central y dispersión son solo una parte de la historia de un conjunto de datos. Es importante siempre considerar el contexto de los datos y cómo se recolectaron, y no confiar únicamente en las medidas de posición y dispersión para tomar decisiones importantes.

Además, es importante tener en cuenta que los valores extremos o influenciados pueden distorsionar la precisión de las medidas de posición y dispersión. Si sospechas que hay valores extremos en tu conjunto de datos, es posible que debas ajustar tus medidas de posición o dispersión para obtener una imagen más precisa de la distribución de los datos.

Ideas para aplicar las medidas de tendencia central y dispersión

A continuación, les presento algunas ideas de cómo se pueden aplicar las medidas de tendencia central y dispersión en situaciones del mundo real:

1. Evaluación del rendimiento de los estudiantes

Si eres profesor o educador, las medidas de tendencia central y dispersión pueden ser útiles para evaluar el rendimiento de tus estudiantes. Puede calcular la media, la mediana y la moda de las calificaciones para determinar la nota "promedio" de tus estudiantes, y la desviación estándar para determinar cuánto varían los resultados.

2. Análisis de encuestas y estudios de mercado

Si estás llevando a cabo una encuesta o un estudio de mercado, las medidas de tendencia central y dispersión pueden ayudarte a evaluar los resultados. Por ejemplo, puedes encontrar la media y la moda de las respuestas de una encuesta para determinar cómo se sienten las personas en general acerca de un tema, y la desviación estándar para evaluar cuánto varían las respuestas.

3. Análisis financiero

Las medidas de tendencia central y dispersión también son útiles para el análisis financiero. Puedes encontrar la media de los ingresos de una empresa para determinar cuál es su ingreso "promedio", y la desviación estándar para evaluar cuánto varían los ingresos. Estas medidas también son útiles para evaluar la rentabilidad y el riesgo asociado con ciertas inversiones.

Cómo calcular las medidas de tendencia central y dispersión

Si quieres calcular las medidas de tendencia central y dispersión en tu propio conjunto de datos, aquí hay algunas formulas para que puedas utilizar:

Cálculo de la media:

 ∑X ---------  N 

Donde ∑X es la suma de los valores en el conjunto de datos, y N es el número de elementos en el conjunto.

Cálculo de la mediana:

Si el número de elementos en el conjunto de datos es impar:

 (Sorting the data) x[(n+1)/2] 

Si el número de elementos en el conjunto de datos es par:

 (Sorting the data) (x[n/2] + x[(n/2)+1])/2 

Donde x es el valor que ocupa el lugar intermedio en el conjunto de datos.

Cálculo de la moda:

Contar la frecuencia de cada valor en el conjunto de datos y elegir el valor que aparece con mayor frecuencia. Si hay más de una moda, hay varias modas en el conjunto de datos.

Cálculo de la desviación estándar:

  ______________________________________ |               ( ∑ (x - μ)^2 )           | | σ = sqrt   _______________________    | |              (   n              )        | |______________________________________| 

Donde x es el valor en el conjunto de datos, μ es la media del conjunto de datos y n es el número de elementos en el conjunto.

Cálculo del rango intercuartílico:

 (Q3 - Q1) 

Donde Q1 es el valor que ocupa el lugar intermedio de los valores debajo de la mediana general y Q3 es el valor que ocupa el lugar intermedio de los valores por encima de la mediana general.

Cálculo de la varianza:

  ______________________________________ |               ( ∑ (x - μ)^2 )           | | σ^2 =   _______________________    | |              (   n              )        | |______________________________________| 

Donde x es el valor en el conjunto de datos, μ es la media del conjunto de datos y n es el número de elementos en el conjunto.

Espero que este artículo les haya sido de ayuda para entender las medidas de tendencia central y dispersión. Estas medidas son muy útiles para entender cómo se distribuyen los datos y pueden ser aplicadas en muchas situaciones del mundo real. ¡Que tengan un buen día!