Medidas De Tendencia Central Media Mediana Y Moda Planeacion

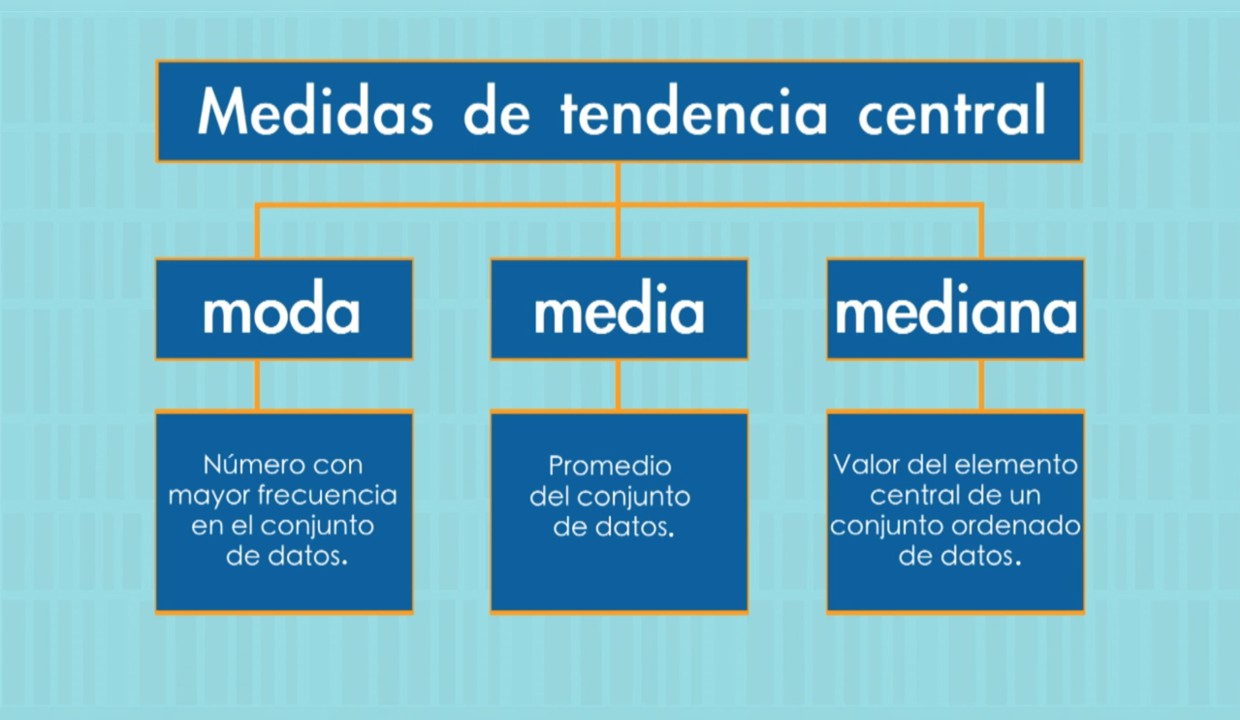
La estadística es una herramienta imprescindible en cualquier campo que requiera la recolección y análisis de datos. En ella, las medidas de tendencia central son un elemento clave para entender la información que se tiene. La media, la mediana y la moda son las medidas más utilizadas en su cálculo. Veamos más sobre las medidas de tendencia central y cómo aplicarlas en diferentes situaciones.

La media

La media es la medida de tendencia central más utilizada. Se calcula sumando todos los valores de una muestra y dividiéndolos por el número total de elementos. La fórmula matemática es la siguiente:

La media es sensible a los valores extremos en los datos, lo que puede hacer que los resultados se distorsionen. Por eso, en algunos casos, es mejor utilizar otras medidas de tendencia central.

La mediana

La mediana es el valor central de una muestra. Se calcula ordenando los datos de menor a mayor y eligiendo el valor que se encuentra en el centro, es decir, el que divide la muestra en dos partes iguales. En caso de que la muestra tenga un número par de elementos, se toma la media aritmética de las dos centrales. La fórmula matemática es:

La mediana es menos sensible a los valores extremos que la media, lo que hace que sea una buena opción para datos que contienen valores atípicos.

La moda

La moda es el valor que más se repite en una muestra. En algunos casos, una muestra puede tener más de una moda, siendo en esos casos una distribución bimodal, trimodal, etc. La fórmula matemática para el cálculo de la moda es la siguiente:

La moda es muy útil para datos que tienen valores repetidos o valores que se concentran en una sola parte de la muestra.

Consejos para aplicar medidas de tendencia central

Para aplicar las medidas de tendencia central, siempre es importante tener en cuenta la naturaleza de los datos que se tienen. Es importante conocer si estos datos presentan valores extremos, si son pocos o muchos, si tienen valores repetidos, entre otros aspectos.

Además, es importante considerar si la muestra es representativa de la población, ya que de lo contrario, los resultados que se obtengan no serán precisos y pueden llevar a conclusiones equivocadas.

Ideas de aplicación de medidas de tendencia central

Las medidas de tendencia central se pueden aplicar en muchos contextos, desde los negocios hasta la medicina. Algunas ideas de aplicación son:

En los negocios

Las empresas pueden utilizar las medidas de tendencia central para analizar sus ventas y tomar decisiones respecto a su estrategia de marketing y precios. Por ejemplo, pueden analizar cuál es el precio medio de los productos que venden y cuál es el producto que tiene una mayor venta.

En la medicina

En la medicina, las medidas de tendencia central se utilizan para analizar datos de pacientes y posibles tratamientos. Por ejemplo, se pueden analizar cuál es la dosis media de un medicamento recetado y cuál es la edad promedio de los pacientes.

En la educación

En la educación, las medidas de tendencia central se utilizan para analizar datos de estudiantes, como las notas y los resultados de exámenes. Por ejemplo, se pueden analizar cuál es la nota media de una clase y cuál es la asignatura que los estudiantes tienen una mayor dificultad.

Cómo calcular medidas de tendencia central

Para calcular las medidas de tendencia central, se puede utilizar software estadístico, como Excel o SPSS. También se pueden hacer cálculos a mano utilizando fórmulas matemáticas, aunque puede ser más complicado y requiere de conocimientos en estadística.

En definitiva, las medidas de tendencia central son una herramienta importante para entender y analizar datos en diferentes contextos. La media, la mediana y la moda son las medidas más utilizadas, y su elección dependerá de la naturaleza de los datos que se tenga, así como del contexto en el que se apliquen.