Medidas De Tendencia Central Media Mediana Y Moda En Estadistica

¡Hola a todos! Hoy quiero hablarles sobre medidas de tendencia central en estadística. Si eres como yo, tal vez hayas tenido un poco de dificultad para entender este tema en la escuela o universidad. Pero no te preocupes, te explicaré de manera sencilla y clara todo lo que necesitas saber.

Media

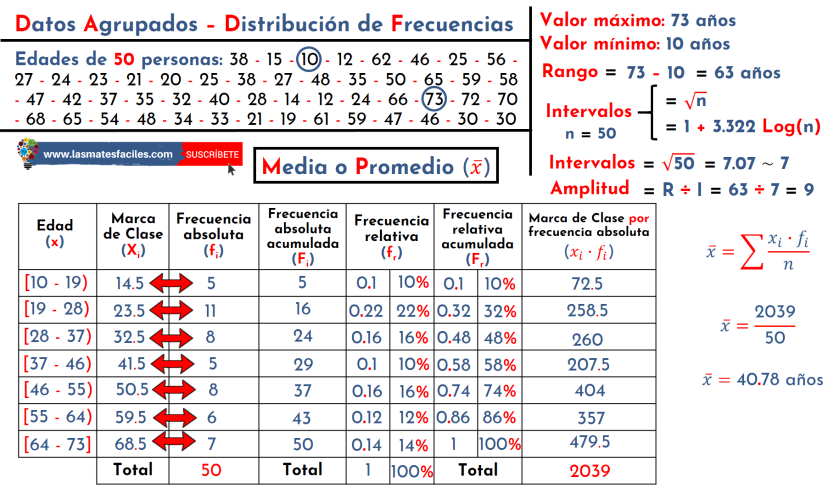
La media es el valor obtenido al sumar todos los valores de una serie de datos y dividir entre el número de datos sumados. Es decir, es el promedio de los datos.

Mediana

La mediana es el valor que se encuentra en la posición central de una serie ordenada de datos. Es decir, si tenemos una lista de datos ordenada, la mediana es el valor que está justo en el centro.

Moda

La moda es el valor que aparece con mayor frecuencia en una serie de datos. Si hay varios valores que aparecen con la misma frecuencia máxima, se dice que la serie de datos tiene varias modas.

Estas tres medidas de tendencia central son muy útiles para resumir y entender un conjunto de datos. Pero hay otras medidas que también pueden ser de gran ayuda.

Rango

El rango es la diferencia entre el valor máximo y el valor mínimo de una serie de datos. Puede ser útil para entender la dispersión de los datos.

Eje medio

El eje medio es el promedio de los dos valores que se encuentran en la posición central de una serie de datos. Es decir, si tenemos una lista de datos ordenada, el eje medio es el promedio de los dos valores que están justo en el centro.

Consejos

Antes de calcular las medidas de tendencia central, es importante tener en cuenta que estas medidas solo son útiles cuando trabajamos con datos cuantitativos. No se pueden calcular para datos cualitativos, como los colores favoritos de las personas. Además, debemos asegurarnos de que los datos sean representativos y no estén sesgados.

Ideas

Si tenemos una serie de datos con valores extremadamente altos o bajos, la media puede no ser una medida adecuada de tendencia central. En estos casos, puede ser más útil utilizar la mediana. También es importante recordar que las medidas de tendencia central no nos proporcionan información sobre la dispersión de los datos.

Cómo

Para calcular la media, debemos sumar todos los datos y dividir entre el número de datos. Para calcular la mediana, debemos ordenar los datos y encontrar el valor central. Si la serie de datos tiene un número par de valores, la mediana es el promedio entre los dos valores del centro. Para calcular la moda, debemos encontrar el valor que aparece con mayor frecuencia. Para calcular el rango, debemos restar el valor mínimo del valor máximo. Finalmente, para calcular el eje medio, debemos encontrar los dos valores centrales y calcular su promedio.

Espero que esta explicación haya sido útil y que ahora tengas una mejor comprensión de las medidas de tendencia central en estadística. ¡No dudes en dejarme tus comentarios o preguntas!