Media Mediana Moda Tendencia Varianza

La estadística es una herramienta fundamental en el mundo actual, siendo indispensable para la toma de decisiones en diversos campos. Una de las ramas más importantes de la estadística son las medidas de tendencia central, las cuales nos permiten obtener una idea general de los datos que estamos analizando.

¿Qué son las medidas de tendencia central?

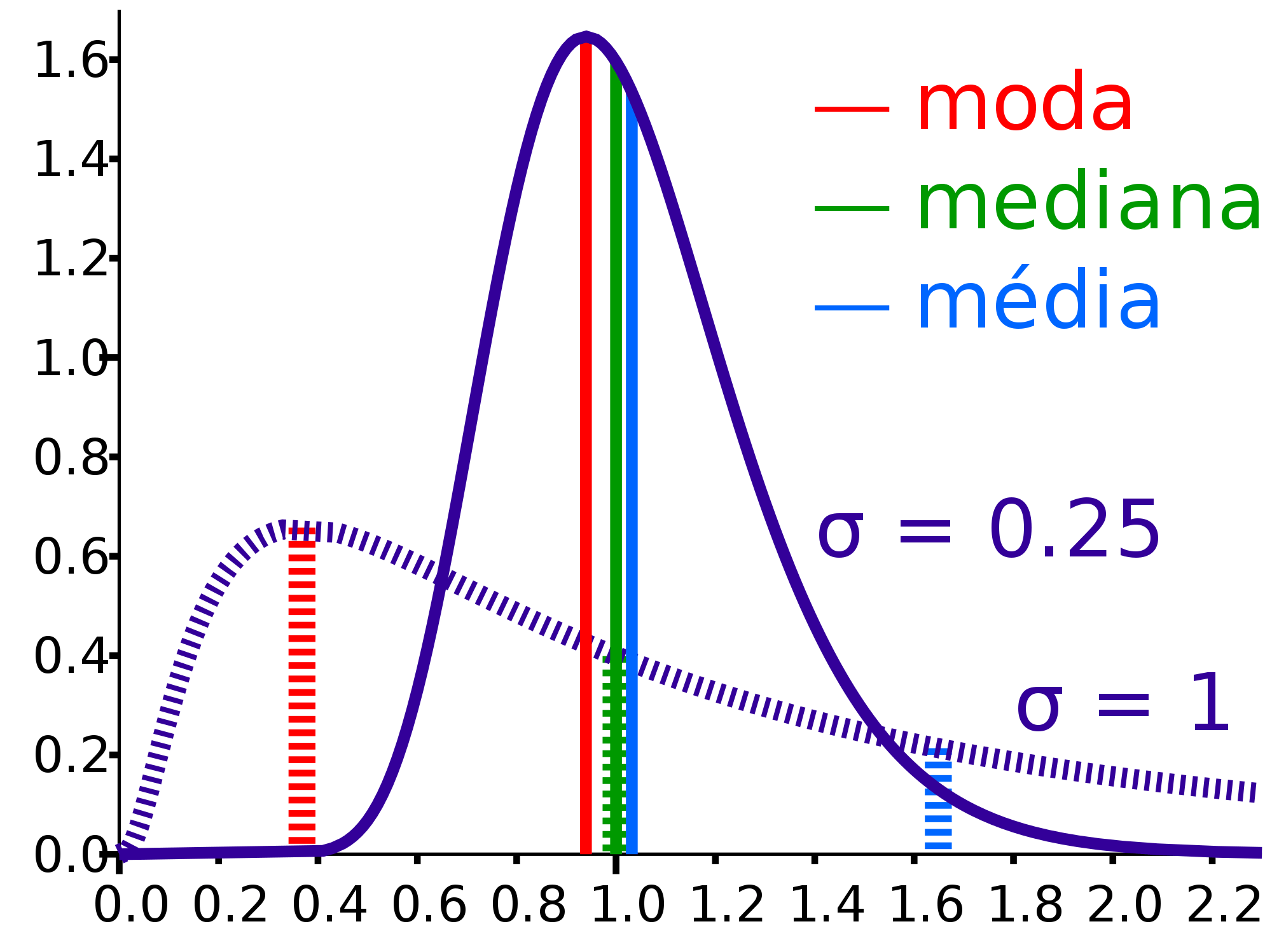
Las medidas de tendencia central son valores que representan el centro de una distribución de datos. Estas medidas nos permiten obtener una idea general de la posición de los datos en la escala de medición. Las tres medidas de tendencia central más comunes son la media, la mediana y la moda.

Media

La media, también conocida como promedio, se obtiene sumando todos los valores de los datos y dividiendo el resultado entre el número total de datos. Esta medida es sensible a los valores extremos y puede verse afectada por ellos.

Para calcular la media de un conjunto de datos, primero se suman todos los valores y luego se dividen entre el número total de datos. Por ejemplo:

Supongamos que queremos calcular la media de los siguientes números: 2, 3, 4, 5, 6.

Para obtener la media, primero sumamos todos los valores:

2 + 3 + 4 + 5 + 6 = 20

Luego, dividimos la suma entre el número total de datos:

20 / 5 = 4

Por lo tanto, la media de los datos es 4.

Mediana

La mediana es el valor que divide a un conjunto de datos en dos partes iguales, es decir, el 50% de los datos se encuentran por encima de la mediana y el otro 50% se encuentran por debajo de ella. La mediana es menos sensible a los valores extremos que la media y es más adecuada para conjuntos de datos con distribuciones sesgadas.

Para calcular la mediana de un conjunto de datos, primero se ordenan los valores de menor a mayor o de mayor a menor. Luego, se busca el valor que se encuentra en el centro de la distribución. Si el número total de datos es impar, este valor será la mediana. Si el número total de datos es par, se calcula la media de los dos valores centrales para obtener la mediana.

Por ejemplo, si tenemos el siguiente conjunto de datos:

2, 4, 6, 8, 10

El valor central es 6, por lo que la mediana de los datos es 6.

En cambio, si tenemos el siguiente conjunto de datos:

2, 4, 6, 8, 10, 12

Los dos valores centrales son 6 y 8. Para obtener la mediana, se calcula la media de estos valores:

(6 + 8) / 2 = 7

Por lo tanto, la mediana de los datos es 7.

Moda

La moda es el valor que se repite con más frecuencia en un conjunto de datos. La moda es útil para identificar los valores más comunes dentro de una distribución y es especialmente útil para datos de tipo discreto.

Para obtener la moda de un conjunto de datos, se cuenta el número de veces que aparece cada valor y se encuentra el valor que se presenta con mayor frecuencia. Si no hay ningún valor que se repita, entonces no hay moda.

Por ejemplo, si tenemos el conjunto de datos:

2, 3, 3, 4, 5, 5, 5, 6

El valor que se repite con más frecuencia es 5, por lo que la moda de los datos es 5.

Consejos para utilizar las medidas de tendencia central

A continuación, te presentamos algunos consejos que pueden ayudarte a utilizar las medidas de tendencia central:

• Comprende cuándo utilizar cada medida: cada medida tiene sus propias fortalezas y debilidades, por lo que es importante elegir la medida correcta para el tipo de datos que estás analizando.
• No te fíes solamente de las medidas de tendencia central: aunque las medidas de tendencia central son importantes, es importante también tener en cuenta la dispersión de los datos, para lo que puedes utilizar medidas de dispersión como la varianza.
• No ignores los valores extremos: aunque la mediana es menos sensible a los valores extremos que la media, estos valores pueden seguir teniendo un impacto significativo en tus resultados. Si sospechas que un valor extremo puede estar afectando a tus resultados, es importante considerar cómo podría afectar a tus resultados antes de ignorarlo por completo.

Ideas para utilizar las medidas de tendencia central

Aquí te presentamos algunas ideas para utilizar las medidas de tendencia central en diferentes situaciones:

• En finanzas: la media y la mediana pueden ser útiles para analizar la rentabilidad de una inversión, mientras que la moda puede ser útil para identificar tendencias en los precios de mercado.
• En marketing: la media y la mediana pueden ser útiles para analizar la satisfacción del cliente, mientras que la moda puede ser útil para identificar los productos que tienen más demanda.
• En investigación médica: la media y la mediana pueden ser útiles para analizar los resultados de un estudio clínico, mientras que la moda puede ser útil para identificar los síntomas más comunes en un grupo de pacientes.

Cómo calcular las medidas de tendencia central

Existen diferentes herramientas que puedes utilizar para calcular las medidas de tendencia central, como Excel o R. Sin embargo, también es útil conocer las fórmulas para poder realizar cálculos a mano si es necesario. A continuación, te presentamos las fórmulas para calcular la media, la mediana y la moda:

Media:

Donde:

• x1, x2, x3, ..., xn son los valores de los datos.
• n es el número total de datos.

Mediana:

Si el número total de datos es impar:

Si el número total de datos es par:

Donde:

• x1, x2, x3, ..., xn son los valores de los datos ordenados de menor a mayor o de mayor a menor.

Moda:

La moda se calcula contando el número de veces que aparece cada valor y encontrando el valor que se presenta con mayor frecuencia.

Por ejemplo, si tenemos el conjunto de datos:

2, 3, 3, 4, 5, 5, 5, 6

Podemos calcular la moda contando el número de veces que aparece cada valor:

• El valor 2 aparece 1 vez.
• El valor 3 aparece 2 veces.
• El valor 4 aparece 1 vez.
• El valor 5 aparece 3 veces.
• El valor 6 aparece 1 vez.

Por lo tanto, la moda de los datos es 5.

En conclusión, las medidas de tendencia central son una herramienta fundamental en la estadística, ya que nos permiten obtener una idea general de los datos que estamos analizando. Es importante comprender cuándo utilizar cada medida, no ignorar los valores extremos y considerar otras medidas como la dispersión de los datos. Además, es útil conocer las fórmulas para realizar cálculos a mano si es necesario.