Definicion Y Caracteristicas De Tendencia Central Media Mediana Moda

En la estadística, se utilizan diversas medidas para obtener una visión más clara y completa de los datos. Las medidas de tendencia central son una de las herramientas más utilizadas en este sentido, y a continuación te hablaremos de algunas de ellas: media, mediana y moda.

Media

La media aritmética o promedio es la medida de tendencia central más conocida. Se calcula sumando todos los valores de un conjunto de datos y dividiendo la suma entre el número total de datos.

La ventaja de la media es que es fácil de calcular y que es sensible a todos los valores. Sin embargo, es vulnerable a los valores extremos, ya que un solo valor atípico puede afectar significativamente el resultado final.

Mediana

La mediana es el valor central de un conjunto de datos. Se calcula ordenando los valores de menor a mayor y escogiendo el valor central en el caso de que el número de datos sea impar. Si el número de datos es par, se toma la media aritmética de los dos valores centrales.

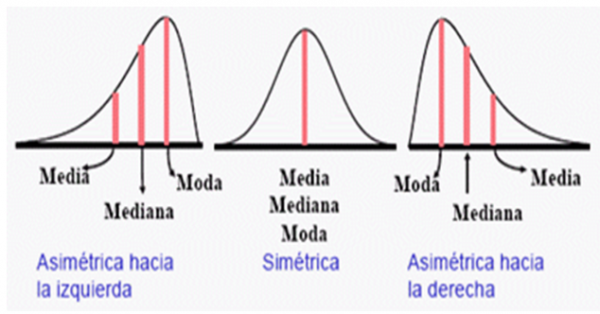
La mediana es más resistente a los valores extremos que la media, ya que sólo se ve afectada por el valor central o por los dos valores centrales en el caso de que el número de datos sea par. Sin embargo, su cálculo es más complejo que el de la media, y no nos ofrece información sobre la distribución de los valores.

Moda

La moda es el valor más frecuente en un conjunto de datos. Se trata del valor que aparece con mayor frecuencia en el conjunto.

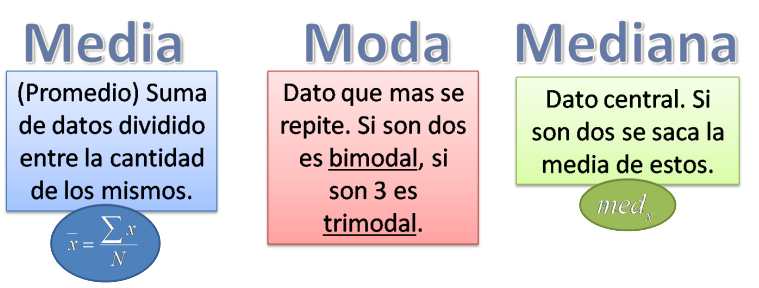
La moda es útil para encontrar patrones en los datos, ya que nos indica cuál es el valor más común. Sin embargo, puede no existir moda en algunos conjuntos de datos, o puede haber varias modas si varios valores tienen la misma frecuencia.

Consejos para utilizar las medidas de tendencia central

Para utilizar las medidas de tendencia central de manera efectiva, es importante seguir los siguientes consejos:

• Conocer los datos con los que se está trabajando. Es importante conocer el tipo de datos con el que se está trabajando, ya que no todas las medidas de tendencia central son aplicables a todos los tipos de datos.
• Tener en cuenta la distribución de los datos. La distribución de los datos afecta a la elección de la medida de tendencia central más adecuada. En general, la media es más adecuada para datos simétricos, mientras que la mediana es más adecuada para datos sesgados.
• Comprobar la influencia de los valores extremos. Los valores extremos pueden tener una gran influencia en la media, por lo que es importante comprobar si existen valores atípicos en el conjunto de datos.

Ideas para aplicar las medidas de tendencia central

Las medidas de tendencia central se utilizan en una gran variedad de ámbitos, desde la investigación científica hasta el análisis de datos empresariales. A continuación, te presentamos algunas ideas para aplicar las medidas de tendencia central:

• En estudios de mercado, se utilizan las medidas de tendencia central para conocer el comportamiento de los consumidores y tomar decisiones en consecuencia.
• En la investigación en ciencias sociales, se utilizan las medidas de tendencia central para obtener una visión general de los datos y analizar las relaciones entre variables. Por ejemplo, se pueden utilizar la media y la mediana para estudiar la distribución de la renta o de la educación en un país.
• En análisis financieros, se utilizan las medidas de tendencia central para analizar los resultados empresariales y tomar decisiones de inversión. Por ejemplo, se pueden utilizar la media y la mediana para analizar los valores de las acciones de una empresa en un periodo determinado de tiempo.

Cómo calcular las medidas de tendencia central en Excel

Una de las herramientas más utilizadas para calcular las medidas de tendencia central es Excel. A continuación, te mostramos cómo calcular la media, la mediana y la moda en Excel:

Media: Para calcular la media en Excel, se utiliza la función AVERAGE. Por ejemplo, si queremos calcular la media de un conjunto de datos que se encuentran en las celdas A1 a A5, escribiríamos en otra celda la fórmula "=AVERAGE(A1:A5)" sin las comillas.

Mediana: Para calcular la mediana en Excel, se utiliza la función MEDIAN. Por ejemplo, si queremos calcular la mediana de un conjunto de datos que se encuentran en las celdas A1 a A5, escribiríamos en otra celda la fórmula "=MEDIAN(A1:A5)" sin las comillas.

Moda: Para calcular la moda en Excel, se utiliza la función MODE. Por ejemplo, si queremos calcular la moda de un conjunto de datos que se encuentran en las celdas A1 a A5, escribiríamos en otra celda la fórmula "=MODE(A1:A5)" sin las comillas.

En conclusión, las medidas de tendencia central son herramientas muy útiles para obtener una visión general de los datos y analizar su distribución. Conociendo las ventajas y desventajas de cada medida, y siguiendo algunos consejos y aplicaciones prácticas, podrás utilizar estas medidas de manera eficaz en cualquier ámbito en el que se utilice la estadística. Recuerda que Excel es una herramienta muy útil para calcular estas medidas de manera sencilla y rápida.