Ejercicios De Medidas De Tendencia Central Media Mediana Y Moda

¡Hola mi gente!

¿Cómo podemos calcular medidas de tendencia central en estadísticas?

En la vida, a veces necesitamos saber qué tan promedio o común es algo en nuestra vida cotidiana, así como en los datos numéricos, para ello existen las medidas de tendencia central. Si bien suena un poco complicado, no te preocupes, ¡podemos guiarte paso a paso para que sigas adelante en el mundo de las estadísticas!

¿Qué es la media?

La media es la suma de todos los datos dividida por el número total de datos en una distribución. Para encontrar la media, simplemente agrega todos los valores juntos y divide el resultado por el número de datos.

Supongamos que tienes las siguientes calificaciones: 90, 85, 80, 95, 100. Para encontrar la media, sumamos los valores y lo dividimos por el número total de valores.

(90 + 85 + 80 + 95 + 100) / 5 = 90

Por lo tanto, la media es 90.

¿Qué es la mediana?

La mediana es el valor medio en una distribución. Es el valor que separa a la mitad superior de la mitad inferior de una distribución.

Para encontrar la mediana, los datos deben estar ordenados de menor a mayor (o de mayor a menor). Si la distribución tiene un número par de datos, la mediana es el promedio de los dos valores medios. Si la distribución tiene un número impar de datos, la mediana es el valor del medio.

Supongamos que tienes las siguientes calificaciones: 90, 85, 80, 95, 100. Para encontrar la mediana, primero ordenamos los datos de menor a mayor.

80, 85, 90, 95, 100

Por lo tanto, la mediana es 90.

¿Qué es la moda?

La moda es el valor más común en una distribución. En otras palabras, es el valor que aparece con más frecuencia en una serie numérica dada.

Supongamos que tienes las siguientes calificaciones: 90, 85, 80, 95, 100, 80. Para encontrar la moda, simplemente buscamos el valor que aparece más veces en la distribución.

El valor 80 aparece dos veces, mientras que todos los demás valores aparecen solo una vez. Por lo tanto, la moda es 80.

Consejos para calcular medidas de tendencia central

Para calcular medidas de tendencia central con mayor precisión, es importante seguir estos consejos:

• Asegúrate de tener todos los datos que necesitas.
• Elimina los valores atípicos o extremos.
• Ordena los datos de menor a mayor o viceversa.
• Utiliza la fórmula correcta para la medida de tendencia central que necesites calcular.

Además, existe otra forma de calcular la media, la mediana y la moda si los datos están agrupados puntualmente, para ello existen las fórmulas siguientes:

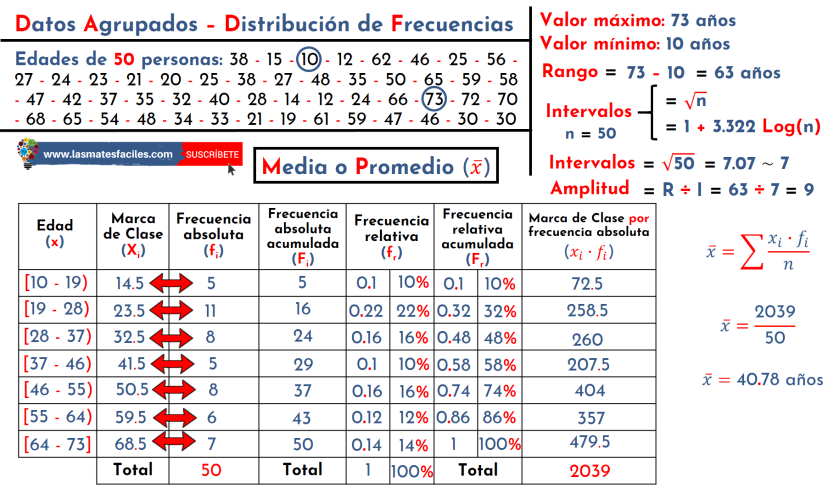
• La media para datos agrupados puntualmente se calcula como la suma de los productos de la frecuencia de cada clase por el valor medio de la misma dividido por la suma de frecuencias de todas las clases.
• La mediana para datos agrupados puntualmente se calcula encontrando el valor de la variable que ocupa la posición N / 2 a partir del valor acumulado de las frecuencias hasta que se alcance o se supere este valor
• La moda para datos agrupados puntualmente es el valor de la variable que tiene la mayor frecuencia absoluta.

Ideas para aplicar medidas de tendencia central en la vida cotidiana

Las medidas de tendencia central son muy útiles en la vida cotidiana para tomar decisiones basadas en datos. Aquí te mostramos algunas formas en las que puedes aplicar estas medidas en la vida diaria:

• Calcular el promedio de calificaciones para decidir si necesitas estudiar más para la próxima prueba.
• Encontrar el valor medio de los precios de un producto para decidir si es asequible o no.
• Calcular la moda del tamaño de la ropa que vendes para asegurarte de tener suficiente inventario en todas las tallas

¿Cómo podemos resolver los ejercicios de medidas de tendencia central?

Comenzamos recordando cómo podemos calcular la media, la mediana y la moda para distribuciones no agrupadas y luego aplicamos las fórmulas para distribuciones agrupadas puntualmente. A continuación, te presentamos algunos ejercicios para que puedas practicar:

1. Encuentra la media, la mediana y la moda de los siguientes datos: 6, 7, 8, 9, 7, 10, 12.

2. Encuentra la media, la mediana y la moda de los siguientes datos agrupados puntualmente:

Clases	Frecuencias
5 - 10	3
11 - 16	4
17 - 22	6
23 - 28	2

3. Encuentra la media, la mediana y la moda de los siguientes datos agrupados puntualmente:

Clases	Frecuencias
1 - 5	10
6 - 10	20
11 - 15	30
16 - 20	10

Conclusión

Las medidas de tendencia central son herramientas estadísticas muy útiles que nos permiten comprender mejor los conjuntos de datos y tomar decisiones mejor informadas en la vida cotidiana. Ya te hemos mostrado cómo calcular la media, la mediana y la moda para distribuciones no agrupadas, así como para distribuciones agrupadas puntualmente. Recuerda que para aplicar estas medidas con mayor precisión, es necesario seguir los consejos que te presentamos, y para resolver ejercicios, es importante practicar y elegir la fórmula correcta para cada caso. ¡Sigue adelante, mi gente, y domina el mundo de las estadísticas!