Modas De Tendencia Central Matematicas

En el mundo de las matemáticas, las medidas de tendencia central juegan un papel importante en el análisis de datos. La medición de la tendencia central es aquella que ayuda a establecer la presencia de una tendencia en los datos, es decir, si los datos tienden a agruparse en torno a un valor específico. Las tres medidas de tendencia central más utilizadas son la media, la mediana y la moda.

La media

La media es probablemente la medida de tendencia central más conocida. Se calcula sumando todos los datos y dividirlos por el número de datos. En otras palabras, es el valor promedio de los datos. La media es útil cuando se desea encontrar un valor que sea representativo de todos los datos en un conjunto, especialmente cuando los datos están distribuidos simétricamente alrededor del valor medio.

Consejos:

• La media es muy sensible a los valores atípicos, por lo que si hay valores extremos en los datos, puede no ser la mejor medida de tendencia central para utilizar.
• La media sólo puede ser utilizada para datos cuantitativos, lo que significa que sólo puede ser calculada para números.

La mediana

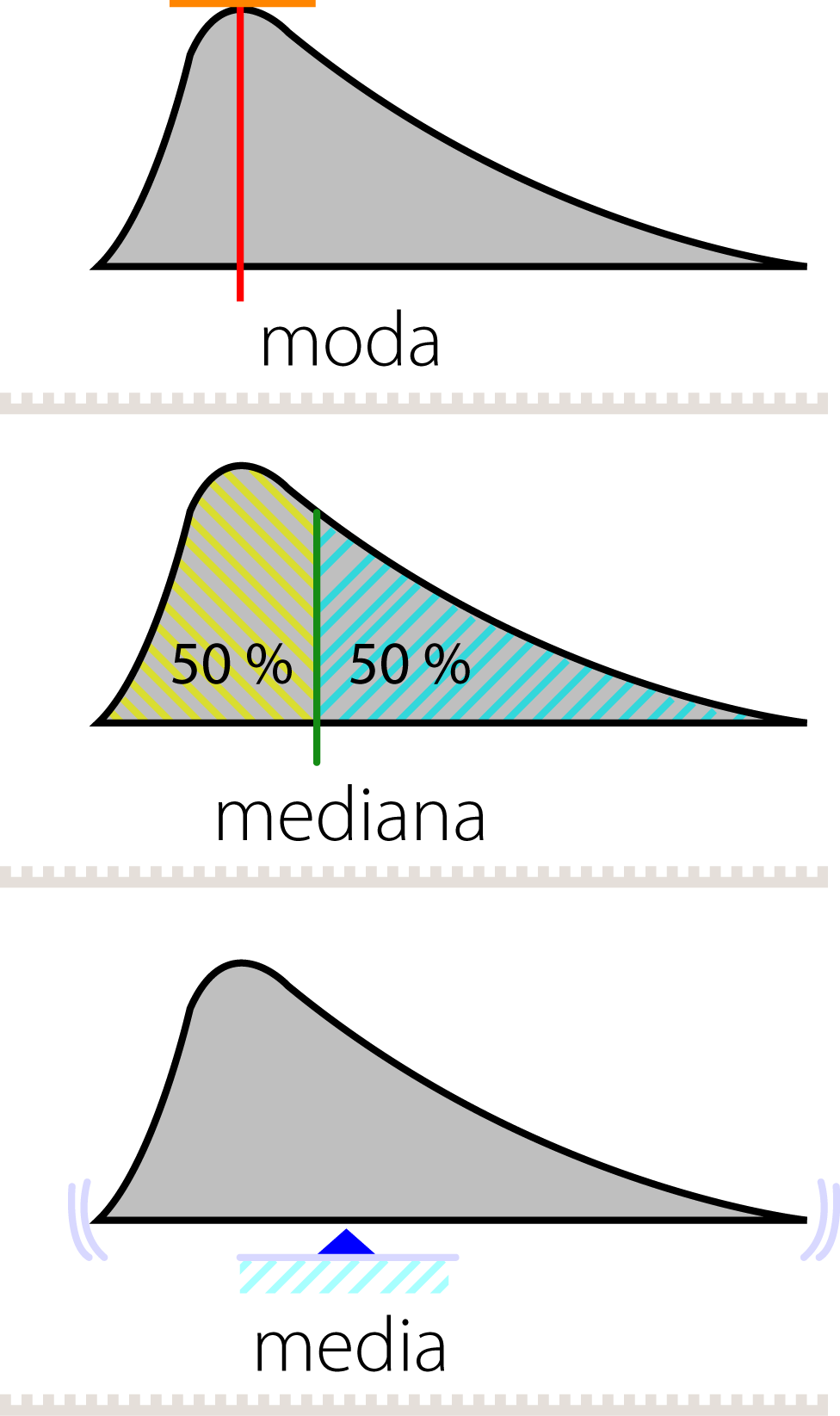
La mediana es el valor en la mitad de los datos ordenados. Es decir, separa los datos en dos partes iguales, dejando la mitad de los datos por encima y la mitad de los datos por debajo del valor de la mediana. La mediana es útil para describir los datos cuando hay valores atípicos o cuando no existe una distribución simétrica en los datos.

Ideas:

• La mediana es menos sensible a los valores atípicos que la media y puede ser una medida de tendencia central más adecuada para utilizar en este caso.
• La mediana puede ser utilizada tanto para datos cuantitativos como para datos cualitativos, lo que significa que puede ser calculada para números y para categorías o grupos.

La moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. La moda es útil para describir los datos cuando se desea saber cuál es el valor que tiene más peso en el conjunto de datos. La moda es especialmente útil cuando se trata de datos cualitativos, tales como preferencias personales, gustos y disgustos, entre otros.

Como:

• La moda no siempre es una medida de tendencia central útil. A veces no puede haber un valor repetido en el conjunto de datos, lo que significa que no hay moda.
• La moda no puede ser utilizada para describir datos numéricos continuos, ya que puede haber muchos valores que tienen la misma frecuencia.

El uso de las medidas de tendencia central

Aunque cada medida de tendencia central tiene su propia finalidad, es importante entender que cada una es útil en diferentes situaciones y que no existe una medida de tendencia central que sea mejor que las demás. Cada medida tiene sus beneficios y limitaciones y depende del conjunto de datos que se esté analizando.

Consejos:

• Es importante elegir la medida de tendencia central correcta para los datos. Si los datos están muy alejados de la media, quizás la mediana sea una medida más adecuada. Si los datos son cualitativos, la moda puede ser la mejor medida de tendencia central.
• Las medidas de tendencia central sólo pueden proporcionar una perspectiva general de los datos. Es importante complementar el análisis con otras medidas estadísticas, tales como la desviación estándar y el rango.

Conclusión

En resumen, las medidas de tendencia central son útiles para resumir y analizar los datos de una manera clara y concisa. Aunque hay tres medidas de tendencia central comunes: la media, la mediana y la moda, cada medida es útil en diferentes situaciones. Es importante entender la finalidad de cada medida para utilizar la más adecuada para los datos en cuestión.