Introduccion Medidas De Tendencia Central Media Mediana Y Moda

¡Hola a todos! Hoy estaremos hablando sobre las medidas de tendencia central, que son la media, la mediana y la moda estadística. Son herramientas muy útiles para analizar y entender grandes conjuntos de datos. Vamos a explorar algunas imágenes para ilustrar las diferentes aplicaciones de estas medidas.

VENTAJAS Y DESVENTAJAS DE LA MEDIA MEDIANA Y MODA ESTADISTICA - SLINGO

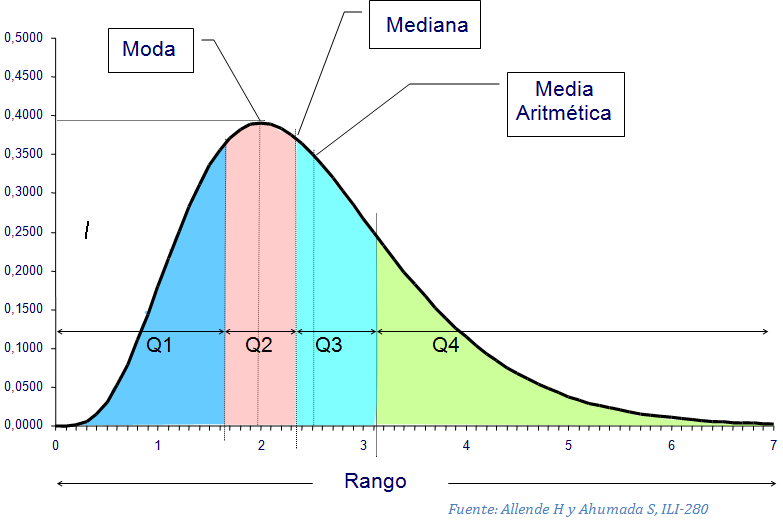
La media estadística es la suma de los valores dividida por la cantidad de valores. Es una medida muy común y puede ser útil para indicar el valor típico de un conjunto de datos. Sin embargo, la media puede verse influenciada por valores extremos o atípicos que no representan el comportamiento general de los datos.

La mediana estadística es el valor medio de un conjunto ordenado de datos. Es útil cuando los datos tienen valores atípicos que afectan la media. La mediana no se ve afectada por estos valores y puede ser una mejor representación del comportamiento general de los datos.

La moda estadística es el valor que aparece con más frecuencia en un conjunto de datos. Es útil para analizar datos discretos, como edades o frecuencias, pero no siempre es aplicable para datos continuos sin valores repetidos.

Al considerar estas diferentes medidas, es importante tener en cuenta la naturaleza de los datos y el propósito del análisis. No hay una medida "correcta" universal, sino que depende de las circunstancias individuales.

FLORERO JARDINES PRECAUCIÓN TENDENCIA CENTRAL MEDIA MEDIANA Y MODA

En esta imagen, vemos cómo las medidas de tendencia central pueden ser útiles en la jardinería y la floricultura. Si queremos asegurarnos de que las flores crezcan de manera uniforme, debemos tener cuidado de no darles demasiada atención a ciertas plantas y descuidar otras. Utilizando la media, mediana y moda estadística, podemos asegurarnos de que estemos proporcionando una cantidad equilibrada de agua, nutrientes y luz a cada planta.

Esto puede aplicarse también en otros aspectos de la vida, como en la distribución de recursos en una empresa o en la gestión de inventarios en una tienda.

APRENDIZAJE DE LA MATEMÁTICA CON USO DE LA TIC: ACTIVIDAD EN GEOGEBRA

La tecnología también puede ayudarnos a entender y aplicar las medidas de tendencia central. En esta imagen, vemos una actividad en Geogebra que permite a los estudiantes visualizar las diferentes medidas y cómo cambian según se agregan o se eliminan datos.

La visualización puede ser una herramienta valiosa para entender conceptos abstractos y hacer más interesante el aprendizaje de las matemáticas.

ESTADÍSTICAS DESCRIPTIVAS Y GRÁFICOS: EJERCICIOS: MEDIA, MEDIANA Y MODA

En esta imagen, vemos ejercicios prácticos que involucran las medidas de tendencia central. Es importante practicar la aplicación de estas medidas para tener una comprensión más profunda de cómo funcionan y cómo se aplican en diferentes situaciones.

Estos ejercicios pueden ser una herramienta valiosa para estudiantes y profesionales por igual.

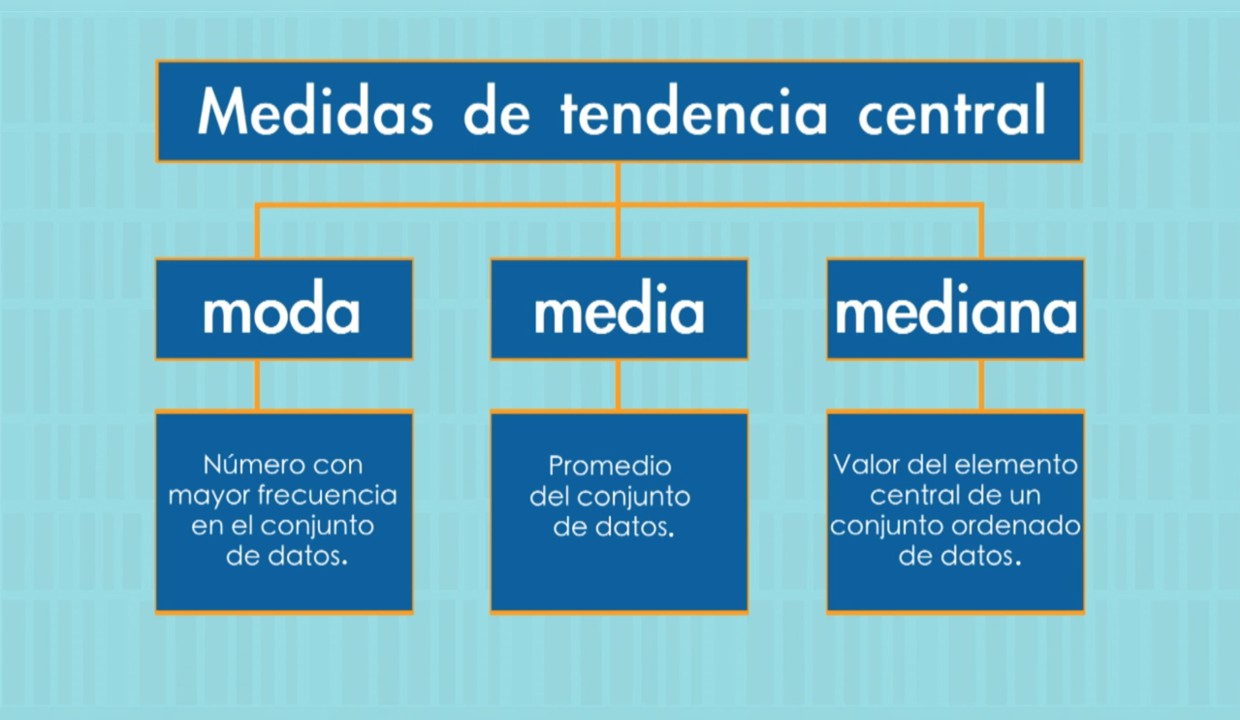
MEDIDAS DE TENDENCIA CENTRAL: UN MAPA CONCEPTUAL

En esta imagen, vemos un mapa conceptual que resume las diferentes medidas de tendencia central y cómo se aplican en diferentes situaciones.

Este mapa puede ser una herramienta valiosa para estudiar y comprender cómo todas las diferentes medidas se relacionan y se diferencian entre sí.

MEDIDAS DE TENDENCIA CENTRAL MEDIA, MEDIANA, Y MODA - YOUTUBE

Para finalizar, presentamos un video en el que se explica cómo utilizar y calcular las medidas de tendencia central. El video es una herramienta muy útil para aprender de manera interactiva y visual cómo se aplican estas medidas.

Recuerda que es importante entender las diferentes aplicaciones de estas medidas y cómo se relacionan con los datos que estamos analizando. Al tener una comprensión más profunda de las medidas de tendencia central, podemos hacer análisis más precisos y tomar decisiones más informadas en muchos aspectos de nuestra vida y trabajo.