Principales Medidas De Tendencia Central Media Mediana Y Moda Ejemplos

Las medidas estadísticas univariantes son de gran importancia en el análisis de datos. Existen diferentes tipos de medidas de tendencia central, tales como la media, mediana y moda. A continuación, se presentarán algunos consejos e ideas para el cálculo de estas medidas y su interpretación en distintos contextos.

Medias estadísticas univariantes

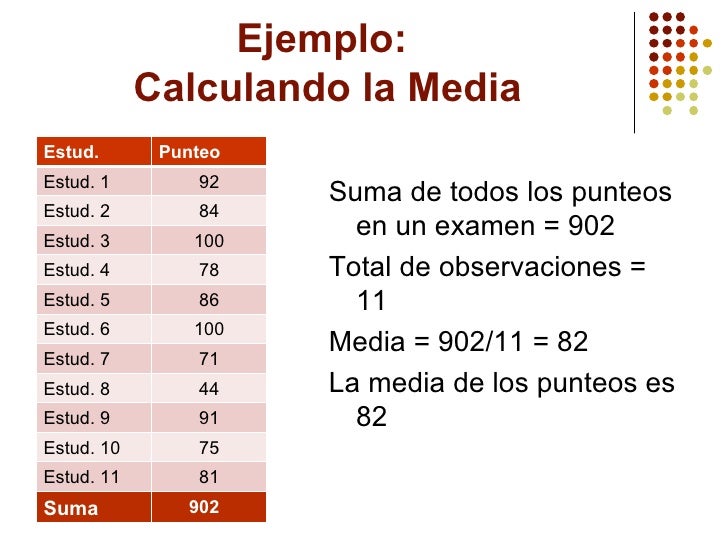
La media es una medida de tendencia central muy utilizada en el análisis de datos. Se calcula sumando los valores de todas las observaciones y dividiendo el resultado entre el número de observaciones. La media es una media aritmética y puede ser influenciada por valores extremos. Se utiliza con mayor frecuencia cuando los datos tienen una distribución normal.

La mediana es la observación que ocupa el lugar central en una serie de datos ordenados. Es menos sensible a los valores extremos que la media, por lo que se utiliza con mayor frecuencia cuando los datos tienen una distribución no normal. En una serie de datos con un número par de observaciones, la mediana se calcula sumando las dos observaciones centrales y dividiendo el resultado entre dos.

La moda es el valor que se repite con mayor frecuencia en una serie de datos. Es útil cuando se busca una observación típica y es especialmente útil en la distribución de frecuencias. Cuando no hay valores repetidos en la serie de datos, no hay moda.

Consejos para el cálculo de medidas de tendencia central

1. Es importante identificar la distribución de los datos antes de seleccionar la medida de tendencia central adecuada.

2. Es necesario ser cuidadoso al seleccionar la medida de tendencia central, ya que cada una tiene su propia interpretación y aplicabilidad.

3. Si hay valores extremos en la serie de datos, es recomendable utilizar la mediana o la moda en lugar de la media.

Ideas para la interpretación de medidas de tendencia central

1. La media es útil cuando se busca una observación representativa del conjunto de datos.

2. La mediana es útil cuando se desea tener una medida de tendencia central que no sea influenciada por valores extremos.

3. La moda es útil cuando se busca la observación más repetida en una serie de datos.

Cómo calcular medidas de tendencia central para datos estadísticos

1. Calcular la media: sumar todos los valores y dividir entre el número de observaciones.

2. Calcular la mediana: ordenar los valores y seleccionar la observación que ocupa el lugar central.

3. Calcular la moda: identificar el valor que se repite más veces en la serie de datos.

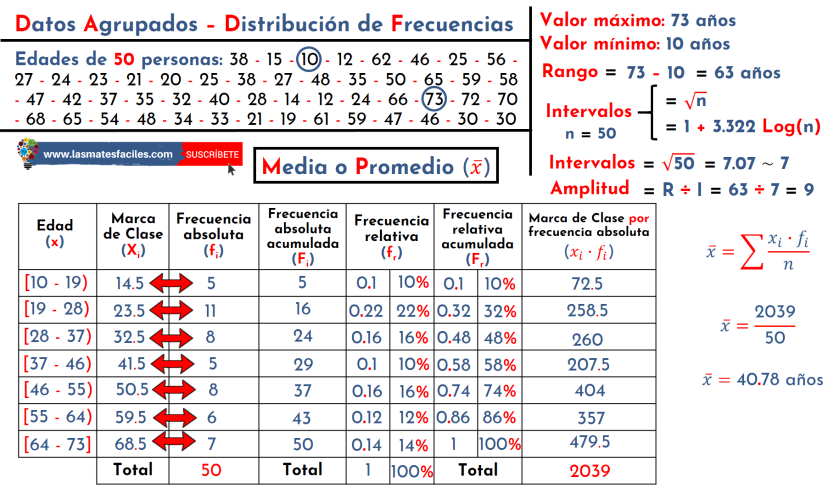
En resumen, es importante seleccionar la medida de tendencia central adecuada para el conjunto de datos. Cada medida tiene su propia aplicabilidad y su interpretación puede ayudar a comprender las características de la distribución de los datos. Se deben tener en cuenta los valores extremos al seleccionar la medida de tendencia central adecuada y se deben seguir los pasos adecuados para calcular la media, la mediana y la moda.