Concepto De Medidas De Tendencia Central Moda

Las medidas de tendencia central y dispersión son fundamentales en la estadística, ya que nos permiten obtener información relevante acerca de un conjunto de datos. En este artículo, te explicaremos todo lo que necesitas saber acerca de estas medidas, así como sus aplicaciones y utilidades.

Medidas de Posición

Las medidas de posición son aquellas que nos permiten ubicar un dato en relación al resto de los datos en un conjunto de información. Las principales medidas de posición son la media aritmética, la mediana y la moda.

Media Aritmética

La media aritmética es la medida de tendencia central más comúnmente utilizada. Se calcula sumando todos los valores de un conjunto de datos y dividiéndolos por el número total de valores. La fórmula para calcular la media aritmética es:

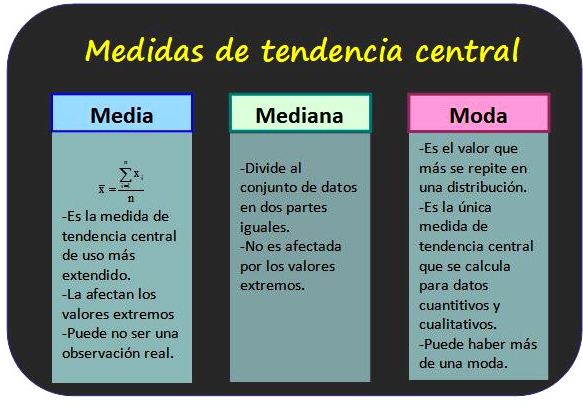
donde n es el número de datos y xi es el valor de cada dato en el conjunto.

Mediana

La mediana es el valor que separa el conjunto de datos en dos partes iguales. Es decir, el 50% de los valores están por debajo de la mediana y el 50% está por encima de ella. Si el número de datos es impar, la mediana es el valor central del conjunto. Si el número de datos es par, la mediana es la media aritmética de los dos valores centrales. Para calcular la mediana, es necesario ordenar los datos de manera ascendente o descendente.

Moda

La moda es el valor que más se repite en un conjunto de datos. Si todos los valores son diferentes, entonces no hay moda. Si hay más de una moda, se dice que el conjunto de datos es bimodal o multimodal.

Medidas de Dispersión

Las medidas de dispersión son aquellas que nos permiten conocer cuánto se alejan los datos individuales de la media de los datos. Las principales medidas de dispersión son el rango, la varianza y la desviación estándar.

Rango

El rango es la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos. El rango es una medida muy simple de dispersión, pero no da información acerca de la variabilidad de los datos en torno a la media.

Varianza

La varianza es una medida de dispersión que nos permite conocer la variabilidad de un conjunto de datos. Se calcula sumando los cuadrados de las diferencias entre cada valor individual y la media del conjunto de datos, y dividiendo la suma por el número de valores en el conjunto menos 1.

Desviación Estándar

La desviación estándar es otra medida de dispersión muy comúnmente utilizada. Se calcula como la raíz cuadrada de la varianza. La desviación estándar indica cuánto se desvían los valores individuales de la media del conjunto de datos.

Consejos Para Interpretar Las Medidas de Tendencia Central y Dispersión

Para obtener una buena interpretación de las medidas de tendencia central y dispersión, es importante tener en cuenta lo siguiente:

• La media aritmética se puede ver afectada por valores atípicos.
• La mediana es más resistente a las fluctuaciones extremas del conjunto de datos y es una buena medida de tendencia central cuando hay valores atípicos presentes.
• La moda es útil para conocer cuál es el valor más frecuente.
• El rango es una medida sencilla de dispersión, pero no nos da información acerca de cómo se distribuyen los datos.
• La varianza y la desviación estándar son medidas más completas de dispersión, ya que nos permiten conocer cómo se distribuyen los datos.

Ideas Para Aplicar Las Medidas de Tendencia Central y Dispersión

Las medidas de tendencia central y dispersión se pueden aplicar en diferentes áreas, como la economía, la medicina, la psicología, entre otras. Veamos algunas ideas prácticas:

• En economía, las medidas de tendencia central y dispersión se utilizan para analizar y predecir el comportamiento de los mercados.
• En medicina, las medidas de tendencia central y dispersión se utilizan para analizar el efecto de los tratamientos en la salud de los pacientes.
• En psicología, las medidas de tendencia central y dispersión se utilizan para analizar la variabilidad de las respuestas de los participantes en un estudio.

Cómo Calcular Las Medidas de Tendencia Central y Dispersión En Excel

Excel es una herramienta muy útil para calcular las medidas de tendencia central y dispersión. Veamos cómo se pueden calcular estas medidas en Excel:

• Para calcular la media aritmética, se utiliza la función AVERAGE.
• Para calcular la mediana, se utiliza la función MEDIAN.
• Para calcular la moda, se utiliza la función MODE.
• Para calcular la varianza y la desviación estándar, se utiliza la función VAR y STDEV respectivamente.

Esperamos que este artículo te haya sido útil para comprender las medidas de tendencia central y dispersión, así como sus aplicaciones en diferentes áreas. Recuerda que estas medidas te permitirán obtener información relevante acerca de los datos que estés analizando.