Definicion Medidas De Tendencia Central Media Mediana Y Moda

16 nov, 2023 Publicar un comentario

¡Hola amigos! ¿Están listos para aprender sobre las medidas de tendencia central? Seguro que sí, porque hoy vamos a hablar sobre la media, la mediana y la moda. Pero primero, porque queremos que entiendan bien qué son estas medidas, les explicaremos brevemente en qué consiste la estadística.

¿Qué es la estadística?

La estadística es la rama de las matemáticas que se encarga de recolectar, analizar e interpretar datos. Es una herramienta muy útil en el mundo actual, ya que nos permite tomar decisiones importantes basadas en la información que tenemos.

Pero, ¿cómo se recolectan los datos? Pues existen diferentes métodos, algunos más precisos que otros, pero en general se utilizan encuestas, muestreos, experimentos, entre otros.

Medidas de tendencia central

Las medidas de tendencia central, como su nombre lo indica, son medidas que indican cuál es el valor central de un conjunto de datos. Es decir, nos proporcionan información sobre el valor típico o representativo de un conjunto de datos.

Existen tres medidas principales de tendencia central: la media, la mediana y la moda. Cada una de ellas se utiliza en diferentes contextos y nos proporcionan información valiosa sobre los datos que estamos analizando.

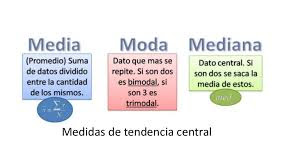
Media

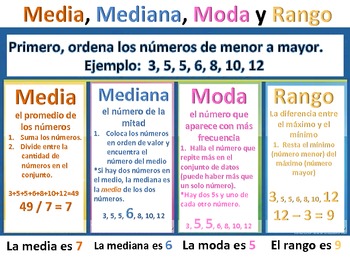
La media es la medida de tendencia central más común. Se calcula sumando todos los valores de un conjunto de datos y dividiendo la suma entre el número de datos. Matemáticamente se representa como:

Media = (x1 + x2 + ... + xn) / n

Donde x1, x2, ..., xn son los datos del conjunto y n es el número de datos.

Mediana

La mediana es el valor que se encuentra en la posición central de un conjunto de datos ordenados de menor a mayor (o viceversa). Es decir, si tenemos un conjunto de datos con 7 elementos, la mediana será el valor que se encuentra en la posición número 4.

En el caso de que el número de datos sea par, se toma la media de los dos valores centrales. Por ejemplo, si tenemos un conjunto de datos con 6 elementos, la mediana será la media de los valores que se encuentran en las posiciones 3 y 4.

Moda

La moda es el valor que más se repite en un conjunto de datos. Es decir, es el dato que tiene la mayor frecuencia en el conjunto.

En algunos casos puede ser que no exista una moda, o que existan varias modas. Por ejemplo, si tenemos el conjunto de datos 1, 2, 3, 3, 4, 5, la moda sería 3.

Consejos para el cálculo de medidas de tendencia central

Para calcular las medidas de tendencia central, es importante seguir ciertos consejos que nos ayudarán a obtener resultados más precisos. Algunos de estos consejos son:

Revisar que los datos estén completos y sean confiables.
Realizar una revisión de los datos atípicos que puedan afectar el resultado.
Seleccionar la medida de tendencia central que mejor se ajuste al conjunto de datos.
Utilizar la medida de dispersión adecuada (como el rango o la desviación estándar) para complementar los resultados.

Ideas para el uso de medidas de tendencia central

Las medidas de tendencia central tienen múltiples aplicaciones en diferentes áreas. Algunas de las ideas para su uso son:

En finanzas, para analizar el rendimiento de una inversión.
En la investigación de mercados, para comprender mejor el comportamiento de los consumidores.
En la medicina, para determinar el tratamiento adecuado para una enfermedad.
En la industria, para identificar los productos más populares y ajustar la producción a la demanda.

¿Cómo calcular medidas de tendencia central en Excel?

Si tienes un conjunto de datos y quieres calcular las medidas de tendencia central en Excel, sigue los siguientes pasos:

Ingresa los datos en una columna de Excel.
Selecciona la celda en la que deseas que aparezca el resultado.
Utiliza la fórmula adecuada para la medida de tendencia central que deseas calcular. Algunas de las fórmulas más comunes son:

Media: =PROMEDIO(rango)
Mediana: =MEDIANA(rango)
Moda: =MODA(rango)

Recuerda que debes reemplazar "rango" por el rango de datos que deseas analizar.

¡Eso es todo por hoy amigos! Esperamos que les haya sido útil esta información sobre las medidas de tendencia central y cómo calcularlas en Excel. Nos vemos en próximos posts.

Ejemplos prácticos

Vamos a ver algunos ejemplos prácticos para que entiendan cómo se aplican las medidas de tendencia central en la vida real.

Ejemplo 1

Imaginemos que tienes una tienda que vende tres tipos de productos: camisas, pantalones y zapatos. Los datos de ventas de los últimos 5 días son:

Camisas: 5, 8, 4, 7, 6
Pantalones: 12, 9, 10, 11, 8
Zapatos: 3, 2, 5, 6, 4

¿Cuál es el producto más vendido?

Para responder esta pregunta, podemos calcular la moda de cada conjunto de datos:

Moda de camisas: no hay moda
Moda de pantalones: no hay moda
Moda de zapatos: 5

Por lo tanto, podemos concluir que los zapatos son el producto más vendido.

Ejemplo 2

Imaginemos que eres un profesor y tienes los siguientes puntajes en un examen de matemáticas:

60, 70, 80, 90, 100

¿Cuál es el puntaje promedio?

Para responder esta pregunta, podemos calcular la media de los puntajes:

Media = (60 + 70 + 80 + 90 + 100) / 5 = 80

Por lo tanto, el puntaje promedio es 80.

Errores comunes al calcular medidas de tendencia central

Aunque las medidas de tendencia central son herramientas muy útiles, hay algunos errores comunes que debemos evitar al analizar datos. Algunos de ellos son:

No considerar los datos atípicos que puedan afectar el resultado.
Utilizar la medida de tendencia central incorrecta para el tipo de datos que se están analizando.
No utilizar una medida de dispersión adecuada para complementar los resultados.

Conclusiones

En resumen, las medidas de tendencia central son herramientas muy útiles en la estadística y nos permiten obtener información valiosa sobre un conjunto de datos. La media, la mediana y la moda son las medidas más comunes, cada una de ellas se aplica en diferentes contextos. Recuerden seguir los consejos para el cálculo correcto de las medidas de tendencia central y evitar los errores comunes.

Esperamos que esta información haya sido útil y nos vemos en el siguiente post.

¿Cómo aplicar medidas de tendencia central en nuestra vida diaria?

Las medidas de tendencia central no solo se aplican en la ciencia, sino también en nuestra vida diaria. Aquí te mostramos algunos ejemplos:

Si vas a comprar frutas y verduras, es importante saber cuál es el precio promedio para evitar pagar de más.
Si estás buscando un lugar para vivir, es importante conocer el costo de los alquileres en la zona para no salirnos de nuestro presupuesto.
Si eres un estudiante y quieres saber cómo te va en una asignatura, puedes calcular el promedio de tus notas para identificar tus fortalezas y debilidades.
Si eres un atleta y quieres conocer tu rendimiento durante una carrera, puedes calcular el tiempo promedio que tardaste en cada kilómetro.

¡Hora de practicar!

Después de haber leído todo esto, ¿te sientes preparado para calcular las medidas de tendencia central por tu cuenta? ¡Te dejamos un ejercicio para que practiques!

Ejercicio

Imaginemos que tienes los siguientes datos:

5, 8, 4, 7, 6, 12, 9, 10, 11, 8, 3, 2, 5, 6, 4

Calcula la media.
Calcula la mediana.
Calcula la moda.

¡Buena suerte!

¿Cómo interpretar las medidas de tendencia central?

Las medidas de tendencia central nos proporcionan información valiosa sobre un conjunto de datos, pero es importante interpretarlas correctamente. Aquí te mostramos algunos consejos:

La media es sensible a los datos atípicos, es decir, si un valor es muy alto o muy bajo, puede afectar significativamente el resultado. Por lo tanto, es importante revisar los datos atípicos antes de interpretar la media.
La mediana es menos sensible a los datos atípicos que la media. Por lo tanto, si hay datos atípicos en el conjunto, es recomendable utilizar la mediana.
La moda es útil cuando se quiere identificar el valor más común de un conjunto de datos. Sin embargo, cuando no hay una moda o hay varias, puede ser difícil interpretar los resultados.

Conclusión final

Esperamos que este post les haya resultado útil y les haya ayudado a comprender mejor las medidas de tendencia central y su aplicación en la estadística. Recuerden que estas medidas nos proporcionan información valiosa que puede ayudarnos a tomar decisiones importantes. ¡Nos vemos en la próxima!

¿Qué aprendimos?

Aprendimos qué es la estadística y para qué se utiliza.
Conocimos las medidas de tendencia central más comunes: la media, la mediana y la moda.
Aprendimos cómo calcular las medidas de tendencia central y cómo aplicarlas en Excel.
Conocimos algunos consejos y errores comunes al calcular las medidas de tendencia central.
Vimos algunos ejemplos prácticos de cómo se aplican estas medidas en la vida real.
Reflexionamos sobre cómo interpretar correctamente las medidas de tendencia central.

¿Cómo aplicar medidas de tendencia central en Excel?

Si quiere calcular las medidas de tendencia central en Excel, estos son los pasos:

Abra Microsoft Excel.
Ingrese los datos que desea analizar en una columna.
Seleccione la celda de Excel donde desea que se muestre el resultado.
Ingrese la fórmula correspondiente a la medida de tendencia central que desea calcular. Puede utilizar estas fórmulas:

Media: =PROMEDIO(rango)
Mediana: =MEDIANA(rango)
Moda: =MODA(rango)

Cambie "rango" por el rango de datos que desea analizar y presione Enter.

Si ha seguido correctamente estos pasos, Excel mostrará la medida de tendencia central que solicitó en la celda correspondiente.

Comprobar respuesta

Ejercicio:

5, 8, 4, 7, 6, 12, 9, 10, 11, 8, 3, 2, 5, 6, 4

Calcula la media.
Calcula la mediana.
Calcula la moda.

Respuestas:

1. Media = (5 + 8 + 4 + 7 + 6 + 12 + 9 + 10 + 11 + 8 + 3 + 2 + 5 + 6 + 4) / 15 = 6.6
2. Mediana = 6
3. Moda = no hay moda

Ropa de Moda