Las Medidas De Tendencia Central Moda Media Aritmetica Secuencia Didactica

En el mundo de la estadística, las medidas de tendencia central son un conjunto de herramientas útiles para analizar y comprender los datos de un conjunto de observaciones. Estas medidas nos permiten describir un conjunto de datos a través de un valor representativo que nos indica la posición central de los mismos. A continuación, presentamos algunas de las medidas de tendencia central más comunes y cómo se calculan.

Media aritmética

La media aritmética es, probablemente, la medida de tendencia central más utilizada en estadística. Esta medida representa el valor medio de un conjunto de datos y se obtiene sumando todas las observaciones y dividiendo esta suma por el número total de observaciones. La fórmula matemática de la media aritmética es:

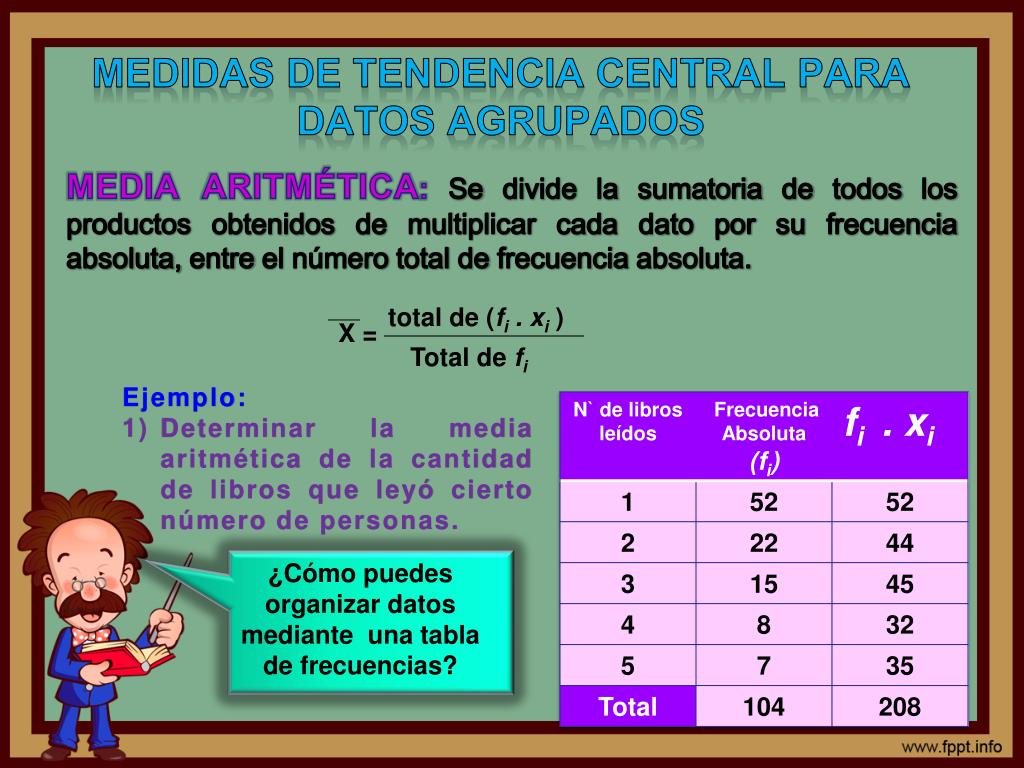
La media aritmética es una medida de tendencia central muy útil y sencilla de calcular. Sin embargo, esta medida puede verse afectada por valores extremos (outliers) que no son representativos del conjunto de datos.

Mediana

La mediana es otra medida de tendencia central muy utilizada en estadística. Esta medida representa el valor central de un conjunto de datos y se obtiene ordenando las observaciones de menor a mayor y seleccionando el valor medio. Si el número de observaciones es par, se toma la media de los dos valores centrales. La fórmula matemática de la mediana es:

La mediana es una medida de tendencia central muy útil cuando el conjunto de datos presenta valores extremos que afectan a la media aritmética. Además, la mediana es una medida resistente a la variabilidad en los datos.

Moda

La moda es otra medida de tendencia central que representa el valor más frecuente de un conjunto de datos. Esta medida se obtiene contando el número de veces que aparece cada valor en el conjunto de datos y seleccionando el valor con mayor frecuencia. Los conjuntos de datos pueden tener una o varias modas, dependiendo de la frecuencia de los valores. La fórmula matemática de la moda es:

La moda es una medida de tendencia central muy útil para conjuntos de datos con valores discretos o categóricos. Sin embargo, esta medida puede no ser representativa de la totalidad del conjunto de datos si existen valores con la misma frecuencia.

Consejos para interpretar las medidas de tendencia central

Al interpretar las medidas de tendencia central, es importante tener en cuenta el tipo de conjunto de datos que estamos analizando y la presencia de valores extremos. Es recomendable utilizar más de una medida de tendencia central para tener una visión completa de la distribución de los datos.

Si el conjunto de datos presenta valores extremos, puede ser conveniente utilizar la mediana como medida de tendencia central en lugar de la media aritmética. Por otro lado, si el conjunto de datos presenta una distribución simétrica, la media aritmética y la mediana deberían ser valores muy similares.

Ideas para aplicar medidas de tendencia central en la investigación científica

Las medidas de tendencia central son una herramienta muy útil en la investigación científica, ya que nos permiten resumir un gran conjunto de datos en una medida única. Estas medidas pueden ser utilizadas para describir la distribución de los datos y para comparar diferentes grupos de observaciones.

En la investigación médica, las medidas de tendencia central son utilizadas para describir la distribución de los valores de una variable en un grupo de pacientes. Por ejemplo, la media aritmética puede ser utilizada para describir el nivel de colesterol en un grupo de pacientes, mientras que la mediana puede ser utilizada para describir la edad de los pacientes.

En la investigación social, las medidas de tendencia central son utilizadas para resumir datos de encuestas y cuestionarios. Por ejemplo, la moda puede ser utilizada para describir el nivel de educación de un grupo de encuestados, mientras que la mediana puede ser utilizada para describir el ingreso promedio de un grupo de encuestados.

Cómo calcular las medidas de tendencia central en Excel

Excel es una herramienta muy útil para el análisis de datos y permite calcular las medidas de tendencia central de manera sencilla. A continuación, presentamos algunos consejos para calcular la media aritmética, la mediana y la moda en Excel.

Cálculo de la media aritmética en Excel

Para calcular la media aritmética en Excel, podemos utilizar la fórmula promedio(A1:A10), donde A1:A10 es el rango de celdas que contiene los valores que queremos promediar. Excel nos devolverá el valor medio de estos valores.

Cálculo de la mediana en Excel

Para calcular la mediana en Excel, podemos utilizar la función mediana(A1:A10), donde A1:A10 es el rango de celdas que contiene los valores ordenados de menor a mayor. Excel nos devolverá el valor central de estos valores.

Cálculo de la moda en Excel

Para calcular la moda en Excel, podemos utilizar la función moda(A1:A10), donde A1:A10 es el rango de celdas que contiene los valores que queremos analizar. Si existen varias modas, Excel nos devolverá el valor con más frecuencia.

En resumen, las medidas de tendencia central son una herramienta fundamental en el análisis de datos y nos permiten describir y comprender los conjuntos de observaciones de manera sencilla. Es importante tener en cuenta las características del conjunto de datos y utilizar más de una medida de tendencia central para obtener una visión completa de la distribución de los datos.