Medidas De Tendencia Central Media Mediana Moda Cuartiles
Imagina que tienes un grupo de amigos que vienen a una fiesta, y quieres saber cuántos dulces debes comprar para que todos se vayan felices. Podrías preguntarle a cada uno cuántos dulces quieren, o podrías hacer una medida de tendencia central para tener una idea más general. ¡Es como un promedio, pero mucho más chévere!
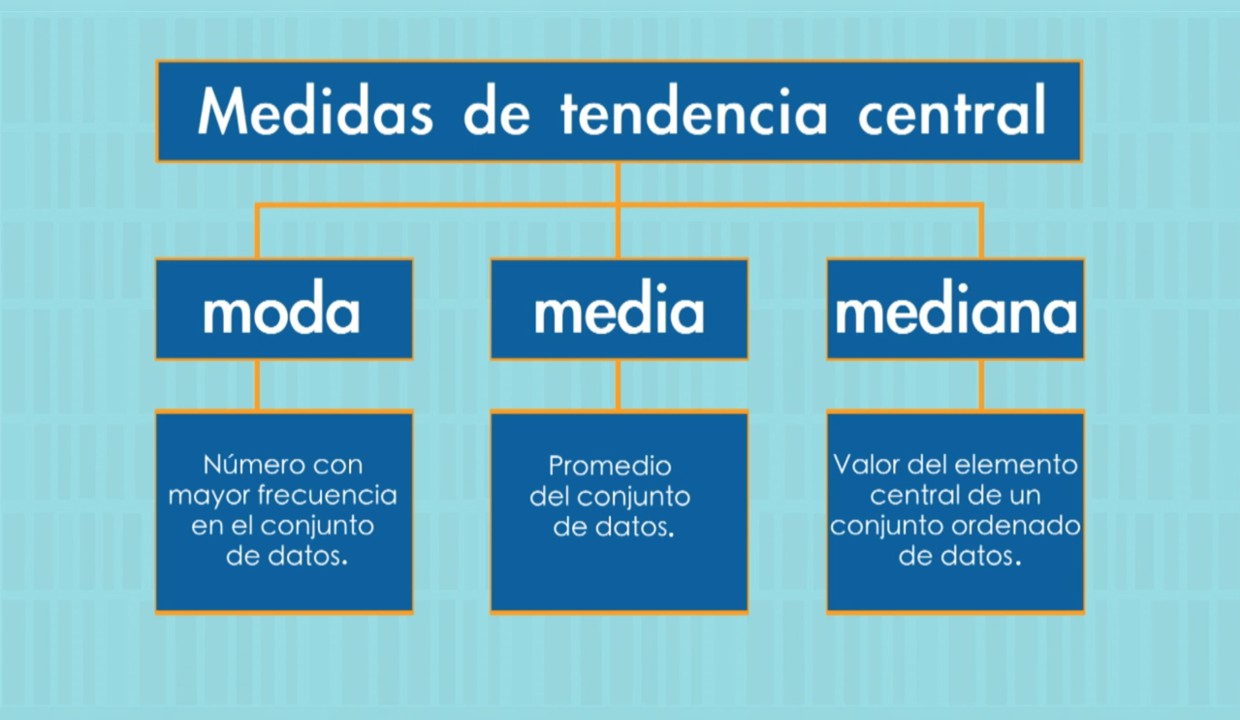
La media
Comencemos con la media (X̄). ¿Cómo se calcula? ¡Es facilísimo! Sumas los valores de todos los dulces que los amigos quieren y luego los divides por el número total de amigos. Aquí va un ejemplo:
Pero ten cuidado, porque hay veces en que la media no es muy útil. Imagina que tuvieras un grupo de amigos con edades muy distintas: si un bebé de 1 año estuviera en la fiesta, su edad afectaría mucho la media, que no reflejaría muy bien la edad promedio de tus amigos. Pero ¡no te preocupes, hay otras medidas de tendencia central que pueden ayudarnos en estos casos!
La mediana
¿Y qué pasa si tienes un grupo de amigos como el que acabamos de mencionar? La mediana es perfecta para estos casos.
La mediana es el número que está justo en el medio cuando los datos se ordenan. Imagina que tenemos estos números:
- 1
- 2
- 3
- 80
Si calculamos la media, nos daría un total de 22:
(1 + 2 + 3 + 80) ÷ 4 = 22
Pero si calculamos la mediana, nos quedaría:
3
¿Ves cómo la mediana sí refleja mejor los datos? ¡Es muucho más intuitiva para entender un grupo de datos que puede tener valores extremos!
La moda
La moda es nuestra última medida de tendencia central. La moda (M) es el dato que más se repite en un conjunto de datos. Esta medida es perfecta si buscas un valor que represente la frecuencia absoluta de un determinado valor. ¡Vamos a ver un ejemplo!

En este ejemplo, podemos ver que la moda es el número 2. ¿Por qué? Porque el número 2 es el que aparece con mayor frecuencia en el conjunto de datos.
¡Pero cuidado! En algunos casos, los datos pueden no tener moda, o puede haber más de una moda. En ese caso, la moda no sería una buena medida de tendencia central para esos datos.
¿Te ha gustado aprender sobre medidas de tendencia central? ¡Espero que sí! Ahora que ya dominas estas medidas, podrás comprar exactamente la cantidad de dulces que necesitas para que tus amigos se vayan felices. ¡Hurra!
Consejos para los que odian las matemáticas
Te entiendo, puede que las matemáticas no sean lo tuyo. Pero no te preocupes, ¡estoy aquí para ayudarte con algunos consejos que harán que todo parezca mucho más fácil!
- Practica en situaciones cotidianas. ¿Cuánto dinero necesitas para comprar la comida de la semana? ¿Cuál es la temperatura media de tu ciudad? Practicar con datos reales te ayudará a comprender mejor las medidas de tendencia central.
- Pide ayuda. ¡No tengas miedo de pedir ayuda si no entiendes algo! Hay muchos recursos en línea y tutorías que pueden ayudarte a entender cualquier concepto de matemáticas.
- No te presiones. Todos aprendemos a nuestro propio ritmo, ¡así que no te desanimes si te toma un poco más de tiempo comprender algo! Lo importante es seguir intentando.
Ideas para impresionar a tus amigos con tus nuevos conocimientos
¿Quieres lucir tus nuevos conocimientos sobre medidas de tendencia central? Aquí van algunas ideas para impresionar a tus amigos:
- Organiza un concurso para adivinar el peso de una calabaza. Calcula la media, la mediana y la moda para los diferentes pesos que los participantes adivinen.
- Crea una encuesta con preguntas sobre las preferencias de comida de tus amigos y calcula las medidas de tendencia central para cada una de las respuestas.
- Pide a tus amigos que adivinen la cantidad de caramelos en un frasco e intenta calcular la media, la mediana y la moda de sus respuestas.
Cómo aplicar estas medidas al mundo real
Las medidas de tendencia central son utilizadas en muchas áreas de nuestra vida. Por ejemplo, en la medicina, los médicos pueden utilizar las medidas de tendencia central para analizar los datos de un grupo de pacientes y tomar decisiones basadas en ellos. En finanzas, las medidas de tendencia central pueden ayudar a prever tendencias del mercado.
Pero las medidas de tendencia central también pueden aplicarse a situaciones más cotidianas. Imagina que estás organizando una venta de garage y quieres ver cuánto puedes esperar ganar. Podrías ver cuánto han ganado otras personas en ventas de garaje similares en tu vecindario y calcular la media, la mediana y la moda de sus ganancias. Con esto, tendrás una idea más clara de cuánto podrías ganar tú también. ¡Así de fácil!
En fin, las medidas de tendencia central son una herramienta muy útil para entender datos y tomar decisiones en situaciones cotidianas. ¡Espero que este post te haya ayudado a entenderlas mejor! Y recuerda, ¡las matemáticas no tienen por qué ser aburridas! Con un poco de humor, todo se hace más ameno.




Publicar un comentario for "Medidas De Tendencia Central Media Mediana Moda Cuartiles"