Medidas De Tendencia Central Media Mediana Moda Ejemplos

¡Hola amigos! Hoy vamos a hablar de un tema muy interesante: las medidas de tendencia central. En estadística, las medidas de tendencia central nos ayudan a entender cómo se distribuyen los datos en un conjunto de observaciones. En este post, vamos a conocer algunos conceptos importantes como la media, la mediana y la moda. También vamos a explorar algunas imágenes y consejos para entender mejor este tema. ¡Así que empecemos!

¿Qué son las medidas de tendencia central?

En estadística, las medidas de tendencia central son valores que representan el centro de un conjunto de observaciones. Es decir, nos dan una idea de la posición de los datos en relación al resto del conjunto. Las tres medidas de tendencia central más comunes son la media, la mediana y la moda.

Media

La media es la medida más común de tendencia central. Se calcula sumando todos los datos y dividiendo el resultado por el número de observaciones. Por ejemplo, si tenemos los siguientes datos: 3, 5, 7, 7, 9, la media sería:

La media nos da una idea de la posición central de los datos. Sin embargo, puede ser influenciada por valores extremos o atípicos en el conjunto, lo que puede hacer que no sea una representación precisa del centro del conjunto.

Mediana

La mediana es una medida de tendencia central que se ubica en el valor medio de un conjunto de observaciones. Es decir, si ordenamos los datos de menor a mayor, la mediana sería el valor que se encuentra en la mitad.

Por ejemplo, si tenemos los siguientes datos: 6, 8, 10, 11, 14, la mediana sería 10. Si tuviéramos un número impar de observaciones, la mediana sería el valor que se encuentra en el medio exacto. Si tuviéramos un número par de observaciones, la mediana sería la media de los dos valores que estén en el centro.

La mediana es menos sensible a valores extremos o atípicos que la media, por lo que puede ser una medida más robusta del centro del conjunto de datos.

Moda

La moda es la medida de tendencia central que representa el valor más frecuente en un conjunto de observaciones. Es decir, es el valor que más se repite. Si todos los valores tienen la misma frecuencia, entonces no hay moda en el conjunto de datos.

Por ejemplo, si tenemos los siguientes datos: 2, 3, 3, 3, 5, 6, 8, la moda sería 3.

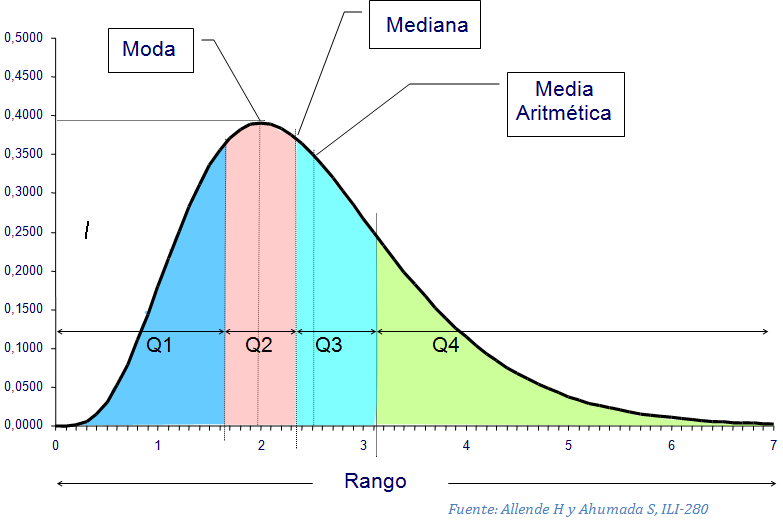
La moda es una medida útil de tendencia central cuando queremos identificar un valor representativo que se presenta con frecuencia en un conjunto de datos. Sin embargo, no es una medida tan útil para conjuntos de datos en los que no haya valores que se repiten con frecuencia.

Consejos para entender las medidas de tendencia central

Para entender mejor las medidas de tendencia central, aquí hay algunos consejos útiles que pueden ayudarte:

• Comprender los conceptos de media, mediana y moda
• Conocer la fórmula para calcular cada medida de tendencia central
• Practicar la resolución de ejercicios que involucren estas medidas
• Entender el efecto de los valores atípicos en cada medida de tendencia central

Ideas para usar las medidas de tendencia central

Las medidas de tendencia central son muy útiles en una variedad de áreas, incluyendo:

• Estudios de mercado para comprender las preferencias de los consumidores
• En el análisis de resultados de pruebas y exámenes
• En análisis financieros para comprender los ingresos y gastos de una empresa

Cómo interpretar las medidas de tendencia central

La interpretación de las medidas de tendencia central depende del conjunto de observaciones que se estén analizando. Si los valores estén agrupados cerca de un valor central, la media, la mediana y la moda serán similares. Si los valores estén más dispersos, las medidas de tendencia central pueden variar significativamente.

Las medidas de tendencia central también son importantes para comprender la forma en que se distribuyen los datos. Si los valores estén agrupados cerca de una medida de tendencia central, esto indica que la distribución del conjunto de datos es simétrica. Si los valores estén más dispersos, la distribución del conjunto de datos puede ser asimétrica o multimodal.

En resumen, las medidas de tendencia central son una herramienta útil e importante en estadística. Nos ayudan a entender cómo se distribuyen los datos en un conjunto de observaciones y nos permiten identificar valores representativos. Espero que este post te haya ayudado a comprender mejor estas medidas y cómo utilizarlas. ¡Hasta la próxima!