Calcular Medidas De Tendencia Central Media Moda Y Mediana

¡Hola a todos! Hoy quiero hablarles sobre un tema que puede resultar un poco intimidante para algunos, pero ¡no se preocupen! Vamos a hablar de las medidas de tendencia central. En estadística, la tendencia central se refiere a la ubicación de los datos dentro de un conjunto de datos y se puede medir utilizando diferentes métodos, que son la media, la mediana y la moda. Para empezar, vamos a explicar brevemente cada una de estas medidas. La media es el promedio de un conjunto de números. Es decir, se suman todos los números y se dividen entre la cantidad de números. La mediana es el número que divide el conjunto por la mitad, es decir, el número que está justo en el centro del conjunto de datos. Finalmente, la moda es el número que aparece con mayor frecuencia en un conjunto de datos. Ahora, vamos a ver algunos ejemplos con imágenes para que sea más fácil de entender.

Ejercicios Medidas De Tendencia Central - Estudiar

En esta imagen podemos ver una tabla de datos para hallar la media aritmética y la mediana.

Media Mediana Y Moda Para Datos Agrupados Puntualmente Datos Agrupados

En esta siguiente imagen se pueden ver datos agrupados puntualmente y agrupados. En la imagen se muestra cómo calcular la media, mediana y moda para ambos tipos de datos.

Media Mediana Y Moda Para Datos Agrupados Puntualmente Datos Agrupados

En esta otra imagen se explica nuevamente cómo calcular la media, mediana y moda para datos agrupados puntualmente y agrupados, con otro ejemplo.

Cómo calcular medidas de tendencia central para datos estadísticos

En esta imagen podemos ver una tabla con los pasos a seguir para calcular la media, la mediana y la moda para un conjunto de datos estadísticos.

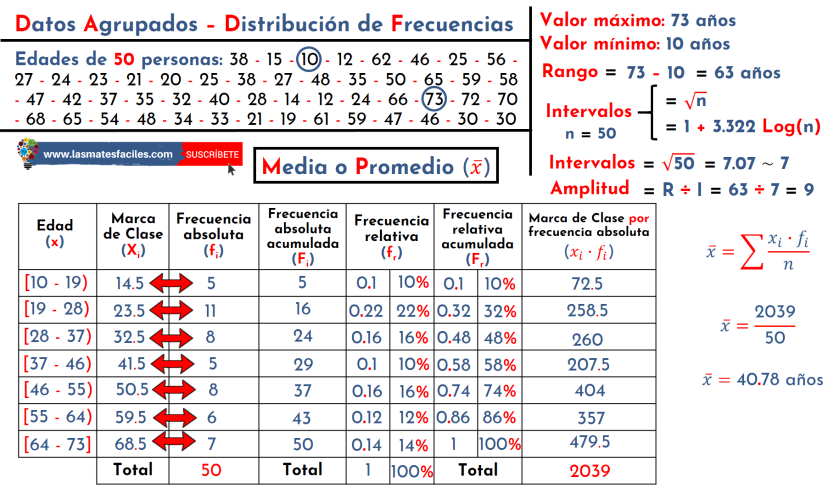
MEDIA MODA MEDIANA EJERCICIOS RESUELTOS

En esta imagen se muestran ejercicios resueltos para calcular la media, la moda y la mediana con diferentes conjuntos de datos.

MEDIDAS DE TENDENCIA CENTRAL

Por último, en esta imagen se muestran diferentes formas de representar las medidas de tendencia central en un conjunto de datos.

Ahora que entendemos los conceptos básicos de media, mediana y moda, ¿cuál de estas medidas deberíamos usar dependiendo de la situación? Si los datos son simétricos y no tienen muchos valores atípicos (números que se alejan mucho del resto de los datos), la media sería una buena medida de tendencia central. Sin embargo, si los datos tienen valores atípicos o son asimétricos, la mediana podría ser mejor. Finalmente, si los datos tienen varios valores que se repiten mucho, la moda sería la mejor medida de tendencia central a utilizar. Espero que ahora tengan una mejor comprensión de las medidas de tendencia central. Recuerden que estas medidas son muy útiles para resumir grandes conjuntos de datos en un solo número que sea representativo del conjunto de datos en general. ¡Hasta la próxima!