Medidas De Tendencia Central Media Mediana Y Moda Conclusion

En el mundo de la estadística, el análisis de medidas de tendencia central es esencial. Esta técnica se utiliza para determinar la posición central de un conjunto de datos. Al identificar la tendencia central de un conjunto de datos, es posible analizar el comportamiento de un fenómeno en cuestión y obtener información valiosa al respecto.

Medidas de tendencia central

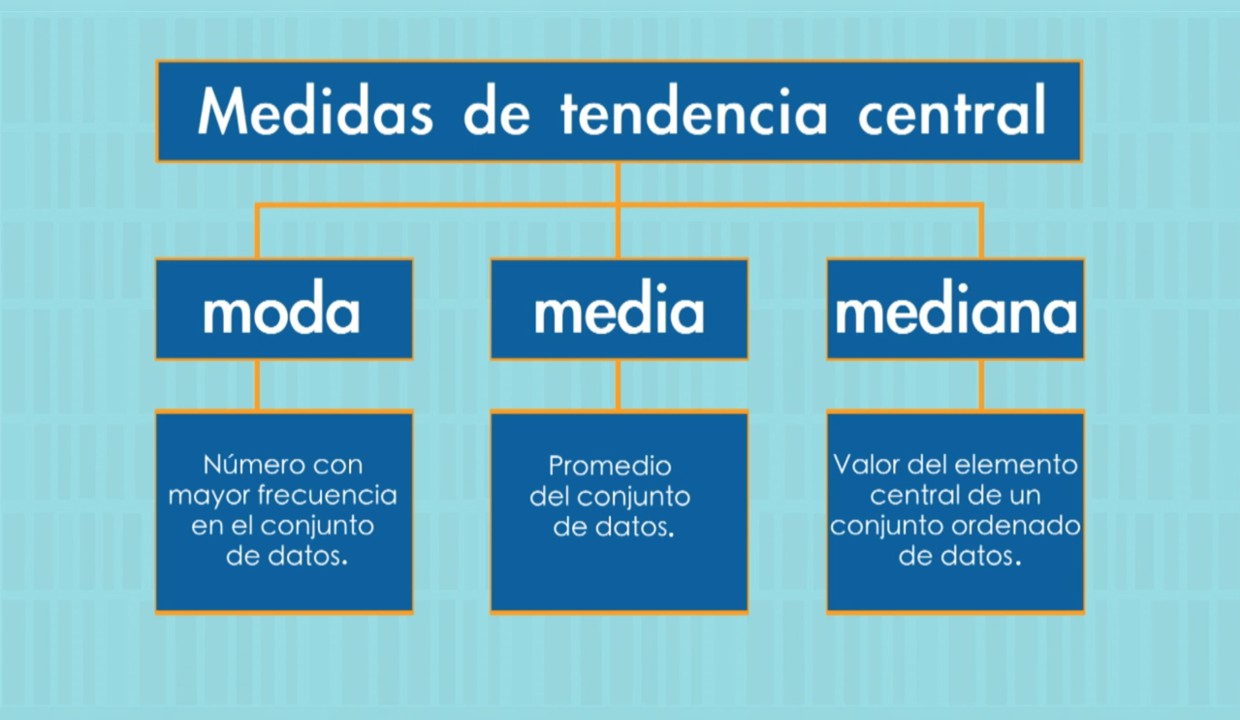
Existen tres medidas de tendencia central comunes: la media, la mediana y la moda.

Media

La media es probablemente la medida de tendencia central más conocida y se define como la suma de todos los valores de un conjunto de datos dividida por el número de valores en el conjunto. La media es una forma sencilla y efectiva de resumir la información contenida en un conjunto de datos, ya que permite obtener una única cifra que representa el comportamiento general del conjunto.

Mediana

La mediana es el valor situado en el centro de un conjunto de datos, es decir, la mitad de los valores se encuentran por encima y la otra mitad por debajo. A diferencia de la media, la mediana no se ve afectada por valores extremos o atípicos en el conjunto de datos, lo que la hace una medida de tendencia central robusta en este sentido.

Moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. La moda puede ser útil en casos en los que el conjunto de datos tiene una distribución desconocida o en los que se desea identificar el valor más repetido en un conjunto de datos grande.

Consejos para el análisis de medidas de tendencia central

Al utilizar medidas de tendencia central para analizar conjuntos de datos, es importante tener en cuenta algunos consejos claves:

1. Comprender el conjunto de datos

Es importante comprender la naturaleza del conjunto de datos, incluyendo la forma en que se recopiló y los tipos de variables específicas que se midieron. Esto ayuda a determinar qué medida de tendencia central es mejor para analizar el conjunto de datos en cuestión.

2. Tener en cuenta valores atípicos

Si hay valores atípicos o extremos en el conjunto de datos, la media puede verse afectada significativamente. En estos casos, puede considerarse el uso de la mediana como medida de tendencia central.

3. Evaluar la distribución del conjunto de datos

Es importante identificar si el conjunto de datos tiene una distribución simétrica o sesgada. Las distribuciones simétricas son aquellas en las que la media, mediana y moda tienen valores similares, mientras que las distribuciones sesgadas tienen valores que se alejan de la media. Es importante tener esto en cuenta al seleccionar la medida de tendencia central adecuada.

Ideas para utilizar medidas de tendencia central en el ámbito laboral

Las medidas de tendencia central pueden ser útiles en una variedad de contextos laborales. Algunas ideas incluyen:

1. Análisis de encuestas

Las encuestas son una forma común en el ámbito laboral de recopilar datos de los clientes o empleados. Al analizar los resultados de una encuesta, las medidas de tendencia central se pueden utilizar para identificar tendencias y puntos clave de interés.

2. Evaluación de rendimiento

Las medidas de tendencia central se pueden utilizar para analizar y comparar el rendimiento de los empleados o equipos en una empresa. Esto puede ayudar a identificar áreas de fortaleza y debilidad y guiar decisiones estratégicas.

3. Análisis de ventas

Las medidas de tendencia central se pueden utilizar para analizar las ventas de productos o servicios. Esto puede ayudar a identificar productos con altas ventas y tendencias generales en el comportamiento del consumidor.

Cómo calcular medidas de tendencia central

El cálculo de las medidas de tendencia central varía según la medida considerada. A continuación, se presentan fórmulas simples para calcular cada medida:

1. Media:

Media = suma de todos los valores en el conjunto de datos / número de valores en el conjunto de datos

2. Mediana:

Si el número de valores en el conjunto de datos es impar, la mediana es el valor situado en el centro del conjunto. Si el número de valores en el conjunto de datos es par, la mediana es la media de los dos valores situados en el centro del conjunto.

3. Moda:

La moda es el valor que aparece con mayor frecuencia en el conjunto de datos.

En conclusión, las medidas de tendencia central son una herramienta valiosa para analizar conjuntos de datos en una variedad de contextos laborales y personales. Para utilizarlas de manera efectiva, es importante comprender el conjunto de datos en sí, tener en cuenta valores atípicos y evaluar la distribución del conjunto de datos. Con una comprensión adecuada de las medidas de tendencia central y cómo utilizarlas, es posible obtener información valiosa que puede guiar decisiones estratégicas y mejorar los resultados en diversos ámbitos.