Medidas De Tendencia Central Y De Dispersión Moda

¡Hola mis queridos hermanos y hermanas! Hoy quiero hablarles sobre las medidas de tendencia central y dispersión. Sé que para muchos de nosotros las estadísticas pueden parecer un poco abrumadoras, pero estoy aquí para ayudarles a entenderlas mejor.

Medidas de dispersión

Empecemos con las medidas de dispersión. Estas medidas nos indican cuán dispersos o esparcidos están los datos. Hay varias medidas de dispersión, pero las más comunes son el rango, la desviación estándar y la varianza.

Rango

El rango es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. Por ejemplo, si estamos hablando de las edades de un grupo de personas y la edad más joven es 20 y la más vieja es 60, entonces el rango sería de 40.

Desviación estándar

La desviación estándar es una medida que nos indica cuánto se desvían los valores de la media. Es decir, si los valores están muy dispersos, entonces la desviación estándar será alta, y si están concentrados alrededor de la media, será baja. Su fórmula puede parecer un poco complicada, pero básicamente mide la distancia promedio de cada dato respecto a la media.

Varianza

La varianza es similar a la desviación estándar pero en lugar de medir la distancia promedio, mide la distancia cuadrática promedio de cada dato.

Medidas de tendencia central

Ahora hablemos de las medidas de tendencia central. Estas medidas nos indican cuál es el valor que mejor representa el conjunto de datos. Las medidas más comunes son la media, la mediana y la moda.

Media

La media es simplemente el promedio de un conjunto de datos. Para encontrar la media, sumamos todos los valores y los dividimos entre el número de datos que tenemos. La media es muy útil para datos que siguen una distribución normal.

Mediana

La mediana es el valor que está en medio de un conjunto de datos cuando están ordenados de menor a mayor. Es decir, si tenemos 5 datos, la mediana sería el tercer valor. La mediana es útil cuando tenemos datos que no siguen una distribución normal.

Moda

La moda es simplemente el valor que más se repite en un conjunto de datos. La moda es útil cuando queremos saber cuál es el valor más común.

Consejos para entender mejor las medidas de tendencia central y dispersión

1. Entender la distribución de los datos

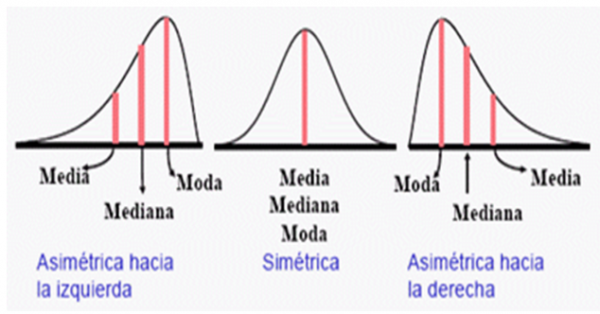
Es importante entender cómo se distribuyen los datos. Si los datos siguen una distribución normal, entonces la media es una buena medida de tendencia central. Sin embargo, si los datos tienen una distribución sesgada, entonces la mediana o la moda pueden ser más apropiadas.

2. Interpretar el valor de la dispersión

El valor de la dispersión nos indica cuán esparcidos están los datos. Si la varianza o la desviación estándar son altas, entonces los valores están muy dispersos. Si son bajas, entonces están muy concentrados alrededor de la media. Es importante entender el valor de la dispersión para interpretar mejor los datos.

3. Usar las medidas de tendencia central y dispersión juntas

Las medidas de tendencia central y dispersión nos dan una vista completa de los datos. Es importante usarlas juntas para entender mejor el conjunto de datos que estamos analizando.

Ideas para utilizar las medidas de tendencia central y dispersión en nuestra vida diaria

1. Analizar nuestras finanzas personales

Las medidas de tendencia central y dispersión son muy útiles para analizar nuestras finanzas personales. Por ejemplo, si queremos saber cuánto gastamos en promedio en comida cada mes, podemos calcular la media de nuestros gastos en comida. Si queremos saber cuánto varían nuestros gastos de un mes a otro, podemos calcular la desviación estándar.

2. Analizar nuestra salud

Las medidas de tendencia central y dispersión también son útiles para analizar nuestra salud. Por ejemplo, podemos calcular nuestra media de peso y altura y compararla con las medias para nuestra edad y género. Si queremos saber cuánto varía nuestro peso de un día para otro, podemos calcular la desviación estándar.

3. Analizar nuestros estudios

Las medidas de tendencia central y dispersión son muy útiles para analizar nuestros estudios. Por ejemplo, si queremos saber cuál es nuestra nota promedio en un semestre, podemos calcular la media de nuestras notas. Si queremos analizar qué tan dispersas fueron nuestras calificaciones en un curso, podemos calcular la desviación estándar.

Cómo calcular las medidas de tendencia central y dispersión

1. Media

Para calcular la media, sumamos todos los valores y los dividimos entre el número de datos. Por ejemplo, si queremos calcular la media de 4, 6, 8, 10 y 12, sumamos los valores y los dividimos entre 5:

(4+6+8+10+12)/5 = 8

2. Mediana

Para calcular la mediana, ordenamos los datos de menor a mayor y encontramos el valor que está en medio. Si tenemos un número par de datos, entonces calculamos la media de los dos valores que están en medio. Por ejemplo, si queremos calcular la mediana de 4, 6, 8, 10 y 12, primero los ordenamos:

4, 6, 8, 10, 12

Luego encontramos el valor que está en medio, que en este caso es 8.

3. Moda

Para calcular la moda, simplemente encontramos el valor que más se repite en un conjunto de datos. Por ejemplo, si tenemos los siguientes datos:

4, 6, 8, 10, 8, 12, 6, 8

La moda sería 8 porque es el valor que más se repite.

4. Desviación estándar

La fórmula para calcular la desviación estándar es:

√((∑(x-μ)²)/n)

Donde x es cada valor en el conjunto de datos, μ es la media y n es el número de datos. Primero calculamos la distancia al cuadrado de cada valor respecto a la media, luego los sumamos y los dividimos entre el número de datos, y finalmente sacamos la raíz cuadrada.

5. Varianza

La fórmula para calcular la varianza es:

((∑(x-μ)²)/n)

Es decir, es la misma fórmula que la desviación estándar pero sin la raíz cuadrada.

Espero que esta información les haya sido útil. Recuerden que las medidas de tendencia central y dispersión son herramientas muy útiles para entender mejor los datos que manejamos en nuestra vida diaria.