Medidas De Tendencia Central Media Mediana Y Moda Datos Agrupados

En el mundo de la estadística, es muy importante tener en cuenta las medidas de tendencia central. Estas medidas nos permiten conocer la posición de un conjunto de datos en relación a su promedio, a su valor más común o a su rango. Conocer estas medidas es fundamental en diferentes áreas como la matemática, la economía, la medicina, la ingeniería y muchas otras disciplinas. En este post, te explicaremos todo lo que necesitas saber sobre la media, la mediana y la moda de un conjunto de datos.

Media

La media es una medida de tendencia central que se calcula a partir de la suma de todos los datos de un conjunto y su división entre el número de elementos totales. Esta medida se representa por la letra griega \u03BC y se utiliza para conocer el valor promedio de un conjunto de datos. La fórmula para calcular la media es la siguiente:

Una de las ventajas de la media es que es muy fácil de calcular y que es una medida muy útil cuando los datos se distribuyen de forma simétrica alrededor de su valor promedio. Sin embargo, la media no es una medida demasiado robusta, ya que puede estar muy influenciada por datos extremos o atípicos que se alejan mucho del valor promedio del conjunto. Este problema se puede solucionar calculando la media truncada o la mediana como medidas de tendencia central.

Mediana

La mediana es otra medida de tendencia central que se utiliza para conocer el valor medio de un conjunto de datos. La mediana es el valor que se encuentra en el centro de un conjunto ordenado de datos, de tal forma que la mitad de los elementos están por encima de la mediana y la otra mitad están por debajo de la mediana. La mediana se representa por la letra Mdn y se calcula según la siguiente fórmula:

En general, la mediana es una medida más robusta que la media, ya que no se ve tan influida por los datos extremos o atípicos. Por ello, si los datos no están distribuidos de forma simétrica alrededor de la media, se suele utilizar la mediana como medida de tendencia central. Sin embargo, la mediana no es una medida tan fácil de calcular como la media, especialmente cuando el conjunto de datos es muy grande o está muy desordenado.

Moda

La moda es una medida de tendencia central que nos permite conocer el valor más común o frecuente de un conjunto de datos. La moda se representa por la letra Mo y se define como el valor que aparece con mayor frecuencia en el conjunto de datos. Si se tiene un conjunto de datos sin valores repetidos, entonces la moda no existe. En algunos casos, un conjunto de datos puede tener más de una moda, lo que se conoce como bimodal o multimodal. La fórmula para calcular la moda es la siguiente:

La moda es una medida muy útil cuando se quiere conocer cuál es el valor más representativo o común de un conjunto de datos. Además, es muy fácil de calcular y se suele utilizar junto a la media y la mediana como medidas de tendencia central. Sin embargo, la moda no es una medida tan robusta como la mediana, ya que puede estar influenciada por datos extremos que no son comunes en el conjunto de datos.

Consejos

• Es importante tener en cuenta que la elección de la medida de tendencia central adecuada dependerá en gran medida de la naturaleza de los datos y del objetivo de la investigación.
• En general, si los datos están bien distribuidos y no hay valores extremos, la media es una buena medida de tendencia central.
• Si los datos están muy sesgados o la distribución es muy irregular, entonces la mediana es una mejor medida de tendencia central.
• Si se quiere conocer cuál es el valor más común o frecuente de un conjunto de datos, entonces se debe utilizar la moda como medida de tendencia central.

Ideas

• Es importante recordar que las medidas de tendencia central son un resumen estadístico de los datos, y que no reemplazan el análisis detallado y cuidadoso de los datos en sí mismos.
• Es recomendable utilizar varias medidas de tendencia central en conjunto, especialmente cuando se realizan investigaciones complejas o con muchos datos.
• Siempre es necesario tener en cuenta la interpretación de los valores de las medidas de tendencia central en el contexto de los datos y del problema en sí mismo.

Cómo calcular las medidas de tendencia central

El cálculo de las medidas de tendencia central depende del tipo de datos que tengamos. Si los datos son no agrupados, entonces se pueden calcular la media, la mediana y la moda con las fórmulas que hemos mostrado anteriormente.

Por otro lado, si los datos están agrupados en intervalos, entonces hay que calcular la media, la mediana y la moda para cada uno de los intervalos y después sumar y promediar los valores. Aquí te dejamos un ejemplo práctico:

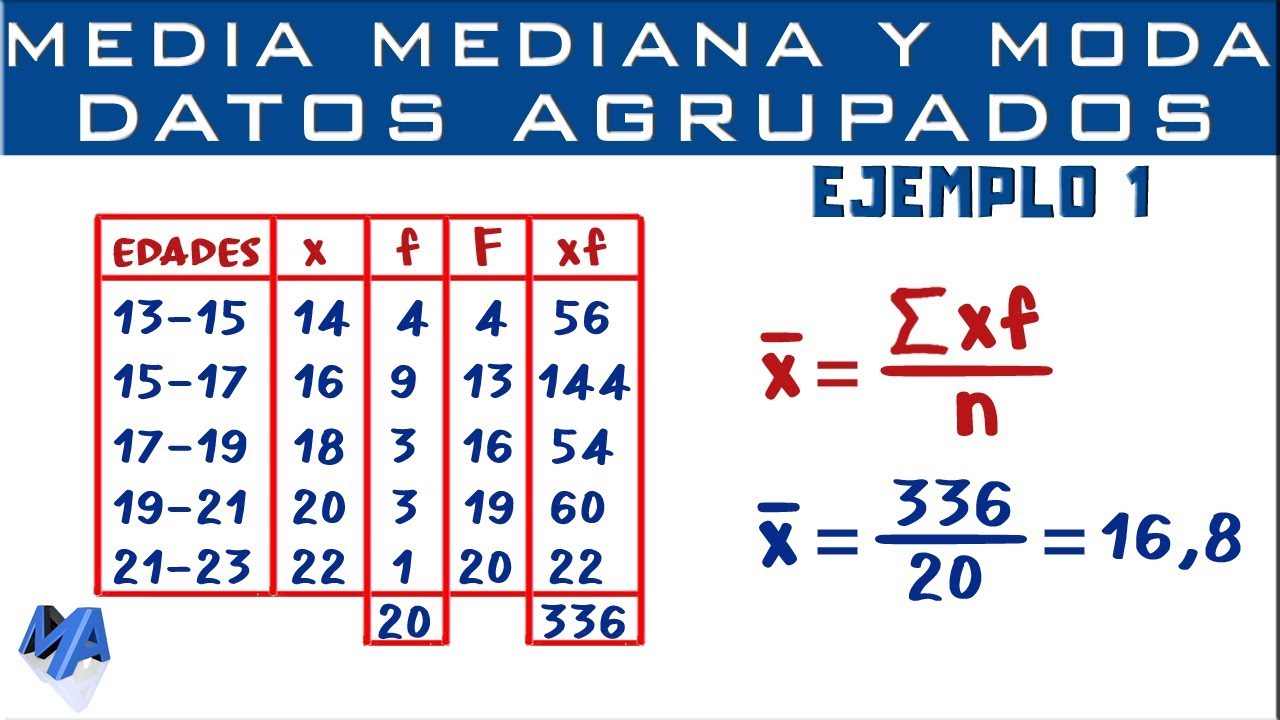
En conclusion, conocer las medidas de tendencia central es fundamental en el mundo de la estadística y las matemáticas. La media, la mediana y la moda son medidas que nos permiten conocer la posición de un conjunto de datos con respecto a su promedio, su valor más común o su rango. Es importante utilizar las medidas adecuadas según la naturaleza de los datos y del objetivo de la investigación, y siempre tener en cuenta la interpretación de los valores en el contexto de los datos y del problema en sí mismo.