Medidas De Tendencia Central Sn Moda

¡Hola a todos! ¡Bienvenidos a nuestro blog de estadística! Hoy hablaremos sobre las medidas de tendencia central en estadística. Si eres estudiante de 4to de ESO, este contenido es para ti.

Medidas de tendencia central

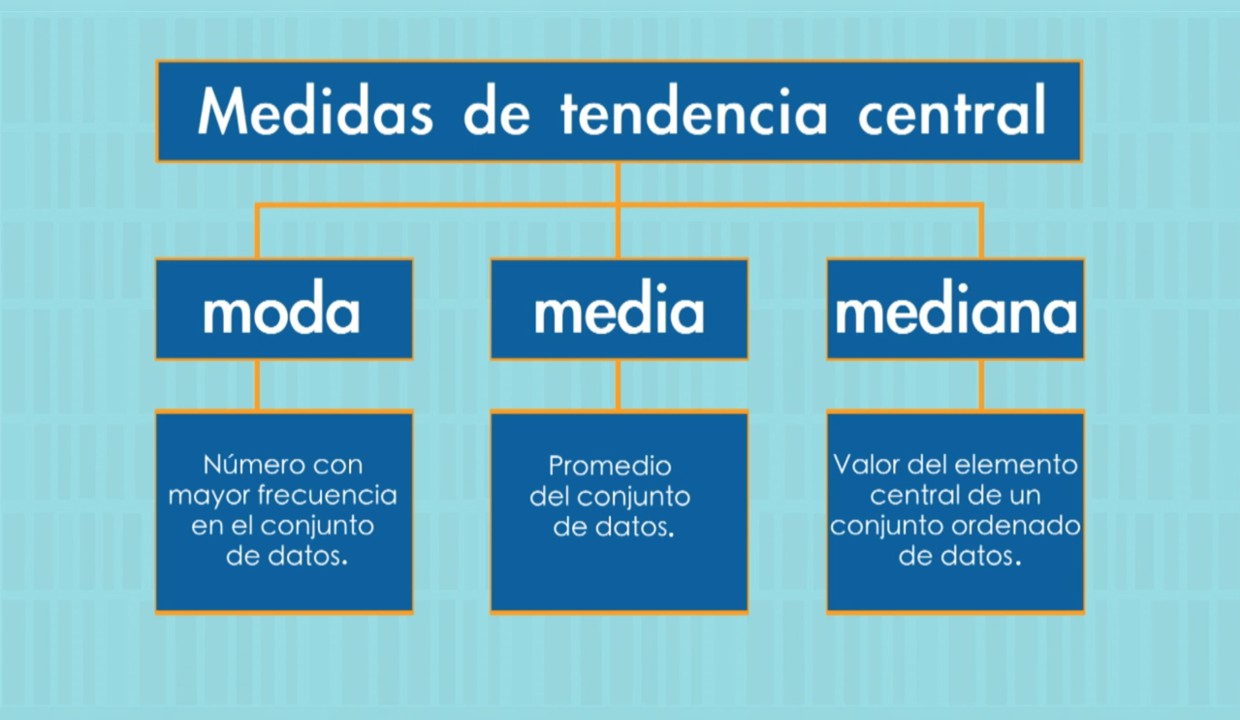
Las medidas de tendencia central son valores que resumen o representan un conjunto de datos. Estas medidas nos permiten obtener una idea general de los datos y representarlos de manera más sencilla. Las medidas de tendencia central más comunes son la media, la mediana y la moda.

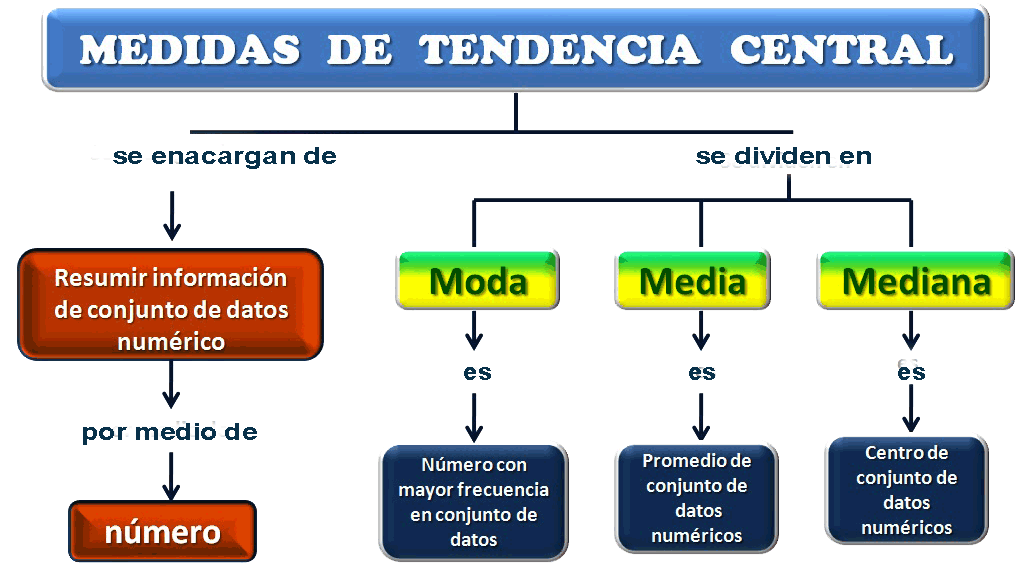
Media

La media es la medida de tendencia central que se obtiene al sumar todos los valores del conjunto y dividir el resultado entre el número total de datos. Por ejemplo, si tenemos los siguientes datos:

• 2
• 4
• 6
• 8
• 10

Para calcular la media, debemos sumar estos valores y dividir entre 5, que es el número total de datos:

(2 + 4 + 6 + 8 + 10) / 5 = 6

Por lo tanto, la media de este conjunto de datos es 6.

Mediana

La mediana es la medida de tendencia central que se encuentra en la posición central de un conjunto de datos ordenados. Para obtener la mediana, debemos seguir los siguientes pasos:

1. Ordenar los datos de menor a mayor o de mayor a menor
2. Si el número total de datos es impar, la mediana es el valor que se encuentra en la posición central. Por ejemplo, en el conjunto de datos 3, 5, 7, 9, 11, el valor que se encuentra en la posición central es 7.
3. Si el número total de datos es par, la mediana es el promedio de los dos valores centrales. Por ejemplo, en el conjunto de datos 2, 4, 6, 8, la mediana es (4 + 6) / 2 = 5.

Moda

La moda es la medida de tendencia central que se obtiene al encontrar el valor que más se repite en un conjunto de datos. Por ejemplo, en el conjunto de datos 3, 5, 7, 7, 9, 11, la moda es 7, ya que es el valor que más se repite.

Consejos para el cálculo de medidas de tendencia central

A continuación, te damos algunos consejos útiles para el cálculo de las medidas de tendencia central:

• Revise los datos antes de calcular las medidas. Asegúrate de que estén completos y que no haya valores atípicos que puedan afectar el resultado.
• Escoge la medida de tendencia central adecuada en función de los datos y el objetivo del análisis. Por ejemplo, la media puede ser sensible a los valores atípicos, mientras que la mediana no.
• Ten en cuenta que las medidas de tendencia central pueden ser engañosas si el conjunto de datos tiene una distribución no simétrica, como una distribución sesgada.
• No utilices las medidas de tendencia central como la única herramienta para el análisis de datos. Es importante complementarlas con otras herramientas estadísticas.

Ideas para ejercitar el cálculo de medidas de tendencia central

La mejor manera de aprender y mejorar el cálculo de las medidas de tendencia central es haciendo ejercicios. Aquí te dejamos algunas ideas:

• Crea conjuntos de datos ficticios y calcula la media, la mediana y la moda.
• Busca ejemplos de conjuntos de datos reales, como datos económicos o deportivos, y calcula las medidas de tendencia central.
• Resuelve problemas que involucren el cálculo de medidas de tendencia central, como calcular el promedio de calificaciones o el tiempo de espera en una cola.
• Analiza conjuntos de datos gráficamente y determina cuál es la medida de tendencia central adecuada para cada caso.

Cómo interpretar las medidas de tendencia central

Conocer las medidas de tendencia central es importante, pero también es fundamental saber interpretarlas correctamente. Aquí te explicamos algunas pautas:

• La media es la medida más comúnmente utilizada y nos indica el valor medio de un conjunto de datos. Sin embargo, es importante tener en cuenta que la media puede verse afectada por valores atípicos.
• La mediana es útil cuando el conjunto de datos tiene valores extremos o una distribución no simétrica. Nos indica el valor que se encuentra en la posición central.
• La moda es la medida que representa el valor que más se repite en un conjunto de datos. Es útil cuando se desea conocer cuál es el valor más común.

Cómo utilizar las medidas de tendencia central en la vida cotidiana

Aunque las medidas de tendencia central son una herramienta fundamental en el análisis de datos, también tienen una amplia aplicación en la vida cotidiana. Aquí te damos algunos ejemplos:

• En el ámbito empresarial, las medidas de tendencia central se utilizan para analizar datos financieros, como el promedio de ventas o el costo de producción.
• En el ámbito médico, las medidas de tendencia central se utilizan para analizar datos de poblaciones, como el promedio de edad de los pacientes o la frecuencia de una enfermedad.
• En el ámbito deportivo, las medidas de tendencia central se utilizan para analizar datos de jugadores o equipos, como el promedio de goles anotados o el tiempo promedio de un partido.
• En la vida cotidiana, las medidas de tendencia central se utilizan para tomar decisiones informadas. Por ejemplo, al comparar precios en el supermercado, podemos utilizar la media de los precios para elegir la opción más económica.

¡Y eso es todo! Esperamos que este post te haya sido útil y que hayas aprendido un poco más sobre las medidas de tendencia central. Recuerda practicar y utilizar estas medidas en tu vida cotidiana. ¡Nos vemos en el próximo post!