Medidas De Tendencia Media Y Moda

¡Bienvenidos a una nueva lección de estadística! Hoy hablaremos sobre las medidas de tendencia central: la media, la mediana y la moda. Estas medidas son muy importantes para entender y analizar los datos. A continuación, les explicaremos en qué consisten cada una de estas medidas y cómo se utilizan en la estadística.

Media

La media (también conocida como promedio) es la suma de todos los valores dividida entre el número de valores. Por ejemplo, si tenemos los siguientes datos: 2, 4, 6, 8 y 10, la media sería:

(2 + 4 + 6 + 8 + 10) / 5 = 6

Es importante tener en cuenta que la media es muy sensible a los valores extremos o atípicos. Por ejemplo, si en el ejemplo anterior cambiamos el valor de 8 por 20, la media sería:

(2 + 4 + 6 + 20 + 10) / 5 = 8.4

Como puede observarse, el valor atípico de 20 ha aumentado significativamente el valor de la media.

Mediana

La mediana es el valor que se encuentra en el medio de un conjunto de datos ordenados de menor a mayor (o de mayor a menor). Para encontrar la mediana, se colocan los datos en orden y se selecciona el valor que está en el medio. Por ejemplo, si tenemos los siguientes datos:

2, 4, 6, 8, 10

La mediana sería 6, ya que es el valor que está en el medio. Si tenemos un conjunto de datos con un número par de elementos, entonces la mediana es el promedio de los dos valores del medio. Por ejemplo:

2, 4, 6, 8

La mediana sería (4 + 6) / 2 = 5

La ventaja de la mediana es que no es sensible a los valores atípicos, por lo que es una buena medida para utilizar cuando existen valores extremos en el conjunto de datos.

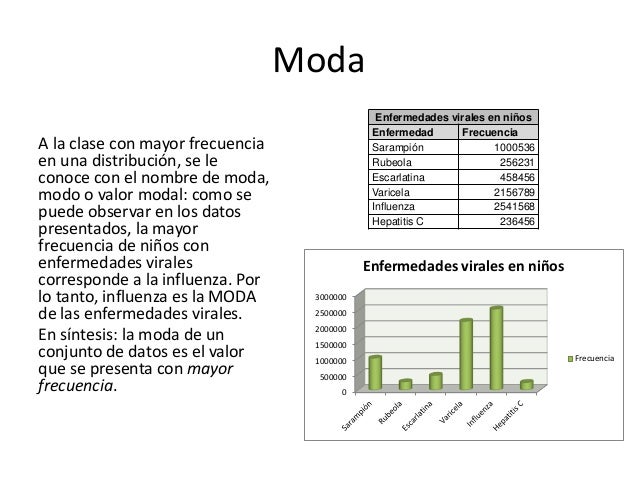
Moda

La moda es el valor que se presenta con mayor frecuencia en un conjunto de datos. Si un conjunto de datos tiene dos valores que se repiten con la misma frecuencia, entonces tiene dos modas y se dice que es bimodal. Si tiene más de dos modas, se dice que es multimodal.

Por ejemplo, si tenemos los siguientes datos:

2, 4, 6, 6, 8, 10, 10, 10

La moda sería 10, ya que es el valor que se repite con mayor frecuencia.

Consejos

Para utilizar correctamente estas medidas de tendencia central, es importante seguir los siguientes consejos:

• Verificar que los datos estén bien definidos y sean correctos.
• Seleccionar la medida de tendencia central adecuada para el conjunto de datos.
• Entender el contexto en el que se utilizan los datos.
• No utilizar la media en conjuntos de datos con valores atípicos.
• Verificar que la moda sea adecuada para el conjunto de datos. En ocasiones, la moda puede no ser representativa del conjunto de datos.
• Combinar las medidas de tendencia central con otras medidas estadísticas para obtener una imagen más completa del conjunto de datos.

Ideas

Las medidas de tendencia central son muy útiles en diversos campos, como la economía, la medicina, la psicología y la educación, entre otros. Algunas ideas para utilizar estas medidas son:

• Calcular la media de las edades de los estudiantes de una escuela para entender la distribución de edades y mejorar la planificación educativa.
• Calcular la mediana del salario de los trabajadores de una empresa para entender la distribución de los ingresos y mejorar las políticas salariales.
• Calcular la moda de las marcas de automóviles preferidas por los consumidores para entender las preferencias del mercado y mejorar la estrategia de ventas.

Cómo utilizar las medidas de tendencia central en Excel

Excel es una herramienta muy útil para calcular las medidas de tendencia central. A continuación, les explicaremos los pasos necesarios para calcular la media, la mediana y la moda en Excel:

1. Seleccionar los datos a analizar.
2. Insertar la fórmula correspondiente para calcular la media, la mediana o la moda.
3. Modificar la fórmula según el tipo de datos y la medida deseada.
4. Observar los resultados obtenidos.

En resumen, las medidas de tendencia central son herramientas muy útiles en la estadística para entender y analizar los datos. La media, la mediana y la moda son las medidas más comunes y cada una tiene sus pros y sus contras. Es importante utilizarlas adecuadamente y en combinación con otras medidas estadísticas para obtener una imagen más completa del conjunto de datos.

¡Esperamos que esta lección les haya sido útil y que ahora puedan utilizar estas medidas de tendencia central en sus propios análisis de datos!

Consejo: Para expresar los datos en gráfico, puedes utilizar los tipos de gráficos que ofrece Excel. En función del tipo de datos y la medida de tendencia central que utilices, podrás elegir entre diferentes gráficos.

Consejo: Si no estás seguro de qué medida de tendencia central utilizar, puedes utilizar las tres y comparar los resultados. De esta forma, podrás elegir la medida que mejor se adapte a tus necesidades.

Ideas: Las medidas de tendencia central también pueden utilizarse en encuestas y estudios de opinión para analizar los resultados y entender las tendencias del mercado.

Cómo: Para calcular la media en Excel, se utiliza la fórmula =PROMEDIO(rango de datos). Para calcular la mediana, se utiliza la fórmula =MEDIANA(rango de datos). Y para calcular la moda, se utiliza la fórmula =MODA(rango de datos). Es importante verificar que los datos estén bien definidos y que la medida utilizada sea adecuada para el conjunto de datos.

Consejo: Para entender mejor las medidas de tendencia central, puedes practicar con diferentes conjuntos de datos y comparar los resultados obtenidos. Esto te ayudará a comprender cómo funcionan estas herramientas estadísticas y cómo utilizarlas en tus propios análisis de datos.

Idea: Las medidas de tendencia central también pueden utilizarse para detectar outliers o valores atípicos en un conjunto de datos. Al comparar los resultados de las diferentes medidas, se puede detectar si existe algún valor que se sale del patrón de los datos y analizarlo en detalle.

Cómo: Para analizar un conjunto de datos con medidas de tendencia central, se pueden utilizar diferentes métodos estadísticos, como la desviación estándar, el coeficiente de correlación o la regresión lineal. Estos métodos permiten obtener una visión más completa y detallada del conjunto de datos analizado.

¡Esperamos que esta lección haya sido útil para entender las medidas de tendencia central en la estadística!