3.2 Medidas De Tendencia Media Mediana Moda Promedio

¿Cómo calcular medidas de tendencia central para datos no agrupados?

Si eres de las personas que busca entender y analizar datos, seguramente has escuchado sobre las medidas de tendencia central. Estas medidas son un conjunto de herramientas matemáticas que nos permiten resumir un conjunto de datos en un solo valor, el cual representa la posición central de los datos.

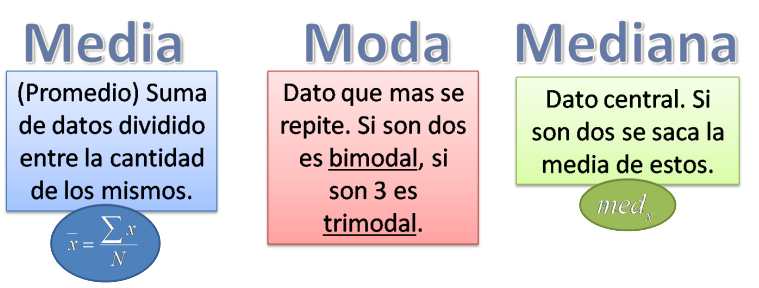
Media aritmética

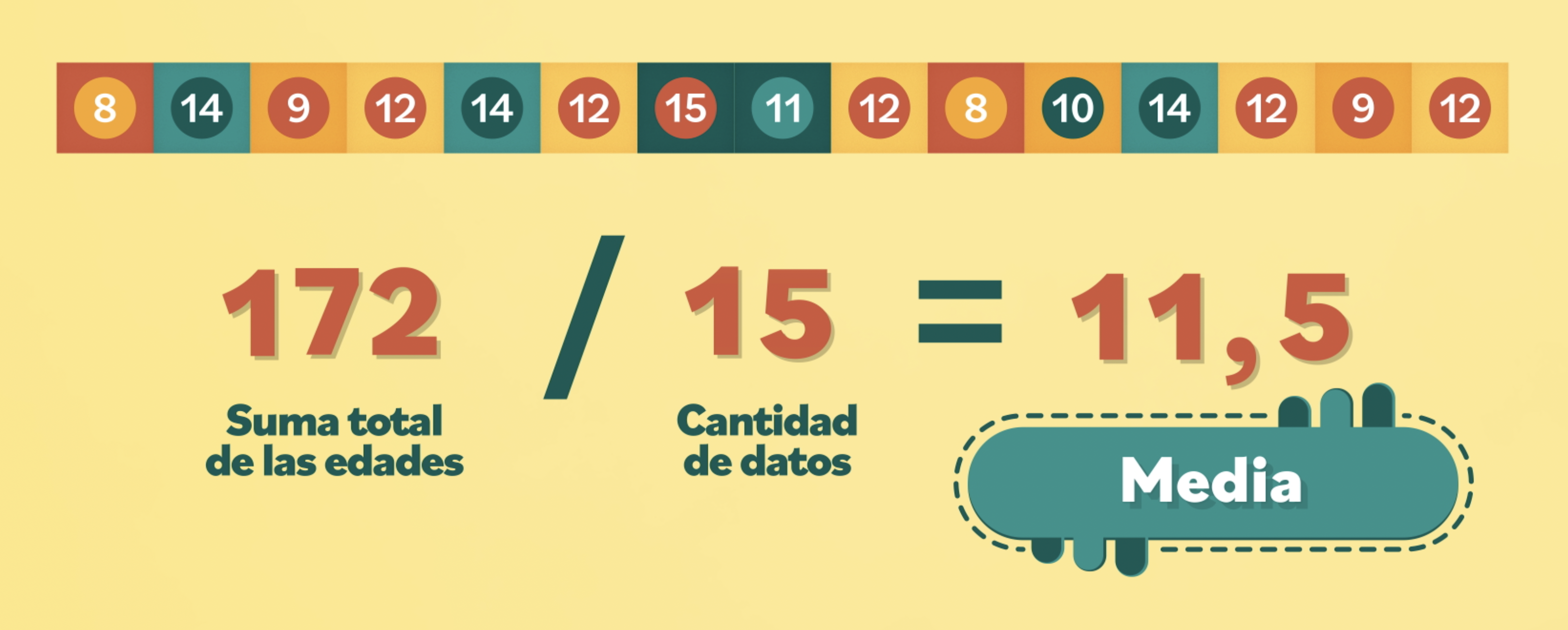
La media aritmética es una de las medidas de tendencia central más utilizadas. Para calcularla, simplemente se debe sumar todos los datos y dividir el resultado entre la cantidad de datos que se tienen.

Por ejemplo, si tenemos los siguientes datos: 2, 4, 6 y 8, la media aritmética sería:

(2 + 4 + 6 + 8) / 4 = 5

Entonces, la media aritmética de esos datos es 5.

Mediana

La mediana es otra medida de tendencia central que resulta interesante en ciertas situaciones. Es el valor que se encuentra en la posición central cuando los datos se ordenan de menor a mayor.

Para calcularla, se deben ordenar los datos de menor a mayor y luego encontrar el valor que se encuentra en el centro. Si la cantidad de datos es par, se debe calcular el promedio de los dos valores centrales.

Por ejemplo, si tenemos los siguientes datos: 2, 4, 6 y 8, la mediana sería:

El tercer valor es 6, por lo tanto, esa es la mediana.

Moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. En algunos casos, puede haber más de una moda. Por ejemplo, en el conjunto de datos 1, 1, 2, 3, 4, 4, hay dos modas: 1 y 4.

Para calcular la moda, es necesario llevar un registro de la cantidad de veces que aparece cada valor. El valor que aparezca con mayor frecuencia será la moda.

Medidas de tendencia central para datos agrupados

En algunos casos, no es posible obtener los datos individuales, sino que estos se presentan en forma de intervalos o clases. En estos casos, se utilizan medidas de tendencia central diferentes.

Media aritmética

Para calcular la media aritmética de datos agrupados, es necesario utilizar las marcas de clase de cada intervalo. La marca de clase es el número que representa la posición central de cada intervalo.

Para calcular la media aritmética de datos agrupados, se utiliza la siguiente fórmula:

media = (∑(marca de clase * frecuencia)) / (∑frecuencia)

Mediana

Para calcular la mediana en datos agrupados, es necesario determinar primero el intervalo que contiene el valor de la mediana. Una vez que se ha encontrado el intervalo, se utiliza la siguiente fórmula para calcular la mediana:

Mediana = L + [(n / 2 - F) / f] * i

Donde:

• L: límite inferior del intervalo que contiene la mediana
• n: cantidad total de datos
• F: frecuencia acumulada anterior al intervalo que contiene la mediana
• f: frecuencia del intervalo que contiene la mediana
• i: amplitud del intervalo

Moda

Para calcular la moda en datos agrupados, se utiliza la clase con mayor frecuencia. Si existen dos o más clases con la misma frecuencia máxima, todas ellas son modas.

Cómo interpretar las medidas de tendencia central

Las medidas de tendencia central son útiles para resumir grandes conjuntos de datos. Sin embargo, no son suficientes para describir completamente los datos. Es importante acompañar la información de las medidas de tendencia central con otras medidas de dispersión, como la desviación estándar y el rango.

Media aritmética

Si la distribución de los datos es simétrica, la media aritmética es representativa del conjunto de datos. Sin embargo, si hay valores atípicos o la distribución no es simétrica, la media puede no ser representativa del conjunto de datos.

Mediana

La mediana es útil cuando los datos no son simétricos o hay valores atípicos. Si la distribución es simétrica, la mediana y la media pueden ser iguales.

Moda

La moda puede ser útil para determinar patrones en los datos y detectar valores atípicos. Sin embargo, no da información sobre la dispersión de los datos.

Consejos para el uso de medidas de tendencia central

Para utilizar correctamente las medidas de tendencia central, es necesario tener en cuenta los siguientes consejos:

• Utiliza medidas de tendencia central apropiadas para el tipo de datos que tienes.
• No te quedes solo con la medida de tendencia central. Complementa la información con medidas de dispersión para obtener una imagen completa de los datos.
• No te guíes solo por las medidas de tendencia central. Analiza los datos en profundidad para detectar patrones y relaciones.

Ideas para el uso de medidas de tendencia central

Las medidas de tendencia central son útiles en una gran variedad de aplicaciones. A continuación, se presentan algunas ideas para su uso:

• En el ámbito empresarial, las medidas de tendencia central son útiles para analizar las ventas, los ingresos y otros datos financieros.
• En el ámbito de la salud, se utilizan medidas de tendencia central para analizar resultados de pruebas médicas y estudios epidemiológicos.
• En el ámbito educativo, las medidas de tendencia central son útiles para analizar resultados de pruebas y exámenes académicos.

Cómo calcular medidas de tendencia central en datos fraccionarios

En algunos casos, puede ser necesario calcular medidas de tendencia central en datos fraccionarios. En estos casos, se utilizan técnicas de cálculo específicas.

Media aritmética

Para calcular la media aritmética en datos fraccionarios, se utiliza la siguiente fórmula:

media = (∑(valor * peso)) / (∑peso)

Donde:

• valor: valor numérico de cada dato
• peso: peso asociado a cada dato

Mediana

Para calcular la mediana en datos fraccionarios, se utiliza una técnica conocida como expansión de símbolos.

Para ello, es necesario ordenar los datos y calcular la suma acumulada de las frecuencias hasta obtener un valor mayor o igual a 0.5. El valor de la mediana se calcula como la suma de la marca de la clase correspondiente a la frecuencia anterior, más la diferencia entre 0.5 y la suma acumulada, dividida por la frecuencia de la mediana.

Moda

Para calcular la moda en datos fraccionarios, se utiliza el mismo método que en datos no fraccionarios. Se registra la cantidad de veces que aparece cada valor y se determina el valor que aparece con mayor frecuencia.

Conclusiones

Las medidas de tendencia central son herramientas matemáticas útiles para resumir grandes conjuntos de datos. Sin embargo, no son suficientes para describir completamente los datos. Es importante acompañar la información de las medidas de tendencia central con otras medidas de dispersión, como la desviación estándar y el rango.

Para utilizar correctamente las medidas de tendencia central, es necesario tener en cuenta el tipo de datos que se tienen y elegir la medida de tendencia central apropiada. Además, no es suficiente utilizar solo las medidas de tendencia central para analizar datos. Es importante analizar los datos en profundidad para detectar patrones y relaciones.

Las medidas de tendencia central son útiles en una gran variedad de aplicaciones, desde el ámbito empresarial hasta el ámbito educativo. Con las técnicas adecuadas, también se pueden calcular medidas de tendencia central para datos fraccionarios.