Que Son Las Medidas De Tendencia Central Media Mediana Moda

¡Hola a todos! Hoy vamos a hablar sobre un tema muy interesante: medidas de tendencia central. Esto puede sonar un poco complicado, pero en realidad es muy útil para entender cómo se distribuyen los datos en una muestra.

Medidas de posición

Comencemos por las medidas de posición, que nos indican dónde se encuentra un valor en relación con el resto de la muestra. Las más comunes son:

• La mediana: que es el valor que divide la muestra en dos partes iguales.
• El cuartil: que divide la muestra en cuatro partes iguales. El primer cuartil es el valor que deja el 25% de los datos a su izquierda, el segundo cuartil es la mediana y el tercer cuartil es el valor que deja el 75% de los datos a su izquierda.
• El percentil: que divide la muestra en 100 partes iguales. Por ejemplo, el percentil 80 es el valor que deja el 80% de los datos a su izquierda.

Con estas medidas podemos tener una idea de dónde se encuentra la mayoría de los datos en la muestra.

Medidas de tendencia central

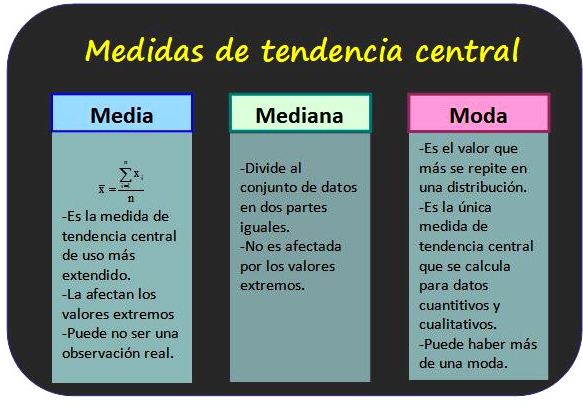
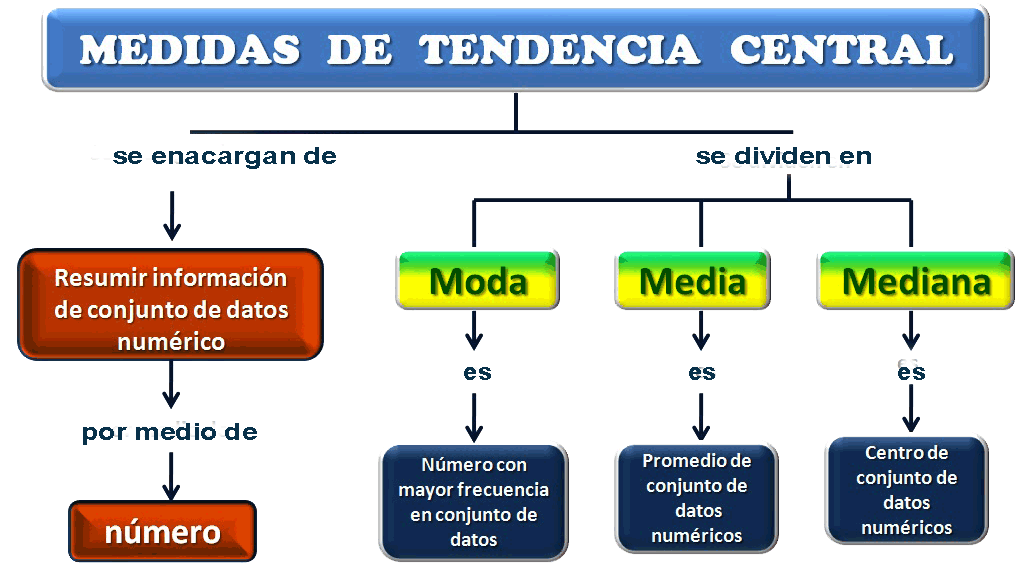
Las medidas de tendencia central nos indican dónde se concentran los datos en la muestra. Las más comunes son:

• La media: que es la suma de todos los datos dividido por la cantidad de datos. Es la medida más común, pero es sensible a valores extremos que pueden sesgarla.
• La mediana: que ya la hemos mencionado antes. Es una medida más robusta que la media, ya que no se ve afectada tanto por los valores extremos.
• La moda: que es el valor que aparece con mayor frecuencia en la muestra. Es útil para datos discretos, pero puede no ser muy representativo para datos continuos.

Con estas medidas podemos tener una idea de dónde se encuentra la mayor concentración de datos en la muestra.

Medidas de dispersión

Pero la distribución de los datos no siempre es uniforme. Puede haber datos muy alejados del resto, o puede haber una gran variabilidad entre los datos. Para medir esto, podemos usar medidas de dispersión, como:

• El rango: que es la diferencia entre el valor máximo y el valor mínimo en la muestra.
• La desviación estándar: que mide la variabilidad de los datos en relación a la media. Si los datos están muy dispersos, la desviación estándar será alta.
• El coeficiente de variación: que mide la dispersión relativa de los datos. Es útil para comparar la dispersión de muestras con diferentes medias.

Con estas medidas podemos tener una idea de cuánto varían los datos en la muestra.

Consejos para interpretar las medidas de tendencia central

Es importante recordar que estas medidas siempre deben ser interpretadas en contexto. Por ejemplo, si estamos analizando la estatura de una población, la media puede ser influenciada por la presencia de atletas o de personas con alguna discapacidad. En ese caso, sería más útil usar la mediana.

También es importante tener en cuenta el tamaño de la muestra. Muestras pequeñas pueden ser muy influenciadas por valores extremos, por lo que las medidas más robustas, como la mediana, pueden ser más útiles en esos casos.

Ideas para aplicar las medidas de tendencia central

Las medidas de tendencia central son muy útiles en diversas áreas, como en la investigación de mercados, en la encuesta de opinión pública y en la evaluación de desempeño de un negocio. Aquí te dejamos algunas ideas de cómo puedes aplicarlas:

• Usa la media para evaluar el desempeño financiero de tu negocio. Puedes calcular la media de los ingresos mensuales para analizar si tu negocio está creciendo o no.
• Usa la mediana para entender el mercado. Si eres dueño de una tienda de ropa, puedes analizar la mediana de los precios de las prendas para tener una idea de en qué rango de precios se encuentra la mayoría de tu competencia.
• Usa la moda para identificar patrones en tus datos. Si tienes un negocio en línea, puedes analizar la moda de los productos más vendidos para entender qué productos son más populares entre tus clientes.

Cómo calcular las medidas de tendencia central

Por último, te dejamos algunas fórmulas para que puedas calcular estas medidas por ti mismo:

Media

Suma de los datos / cantidad de datos

Mediana

Si la cantidad de datos es impar, la mediana será el valor que se encuentra en el centro de la muestra. Si la cantidad de datos es par, la mediana será la media de los dos valores centrales.

Moda

El valor que aparece con mayor frecuencia en la muestra.

Desviación estándar

√[(Σ(x-avg)²)/n]

Donde x es cada valor en la muestra, avg es la media aritmética de la muestra, y n es la cantidad de datos en la muestra.

Coeficiente de variación

(Desviación estándar / media) x 100%

Esperamos que estos consejos, ideas y fórmulas te sean útiles para entender y aplicar las medidas de tendencia central. ¡Gracias por leer!