Medidas De Tendencia Central Moda Si Hay Mas De Uno

¡Hola a todos! Hoy quiero hablarles sobre un tema muy interesante y útil: las medidas de tendencia central. Si te interesa la estadística y las matemáticas, este post es para ti. Primero, ¿qué son las medidas de tendencia central? Son estadísticos que nos ayudan a entender la distribución de los datos en un conjunto de observaciones. En otras palabras, nos dan una idea de la "typicalidad" de los datos. Hay tres medidas de tendencia central comunes: la media, la mediana y la moda. Aquí te explicaré brevemente cada una de ellas. La media es la suma de todos los datos dividida por el número de observaciones. Es una medida muy útil cuando los datos están distribuidos en forma de campana o Gaussiana, es decir, cuando la mayoría de los datos se encuentran cerca del centro. Si hay unos pocos valores extremos, la media puede ser sesgada. La mediana es el valor que está en el medio de un conjunto de datos ordenados. Esta medida es muy útil cuando los datos no están distribuidos en forma de campana, sino que hay muchos valores extremos. La mediana nos da una idea de lo que es típico en el conjunto de observaciones. La moda es el valor que aparece más frecuentemente en un conjunto de datos. Es muy útil cuando algunos valores se repiten con mucha frecuencia. Por ejemplo, si quieres saber qué talla de zapatos es la más común entre tus amigos, la moda te dará la respuesta. Ahora que sabes lo que son las medidas de tendencia central, te mostraré algunas imágenes para que puedas comprenderlas mejor.

Imagen 1: florero Jardines Precaución tendencia central media mediana y moda

En esta imagen podemos ver cómo se calculan la media, la mediana y la moda en un conjunto de datos. La media se calcula sumando todos los valores y dividiéndolos por el número de observaciones. La mediana es el valor que está en el medio de los datos ordenados, y la moda es el valor que aparece con mayor frecuencia.

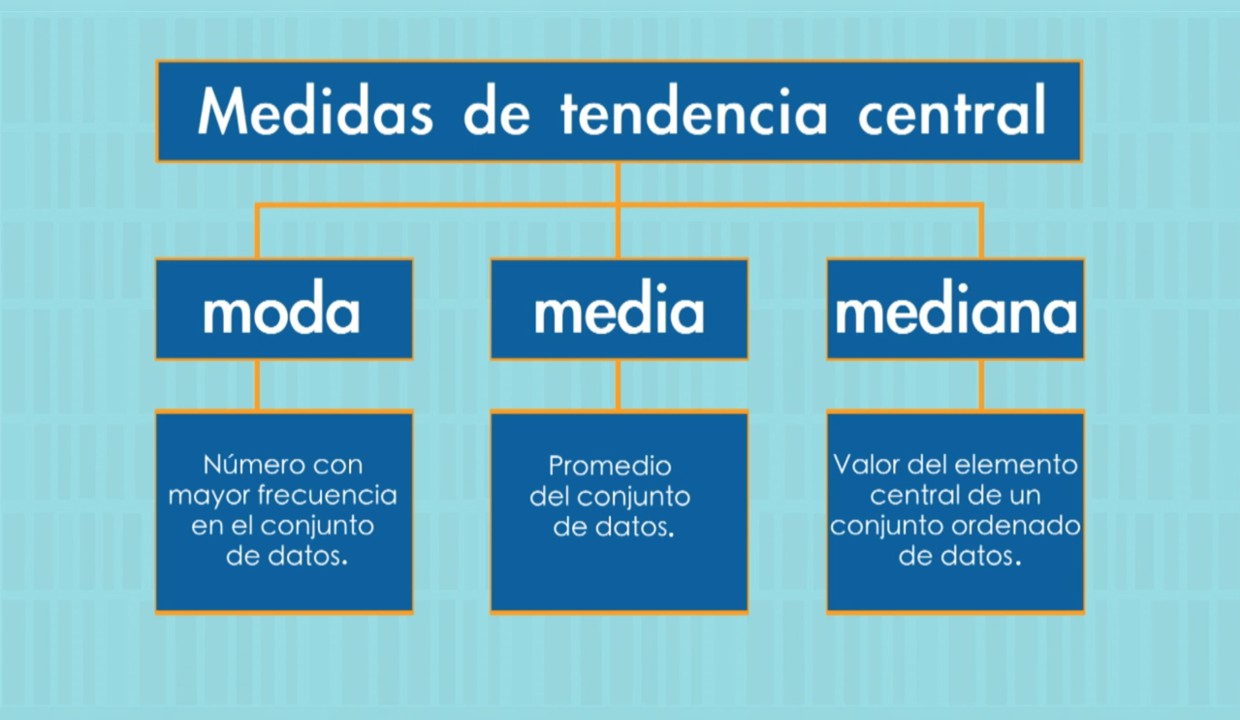
Imagen 2: MATEMÁTICA

En esta imagen podemos ver un gráfico que muestra la distribución de un conjunto de datos. Podemos ver que los datos están distribuidos en forma de campana, lo que sugiere que la media sería una medida adecuada para este conjunto de observaciones.

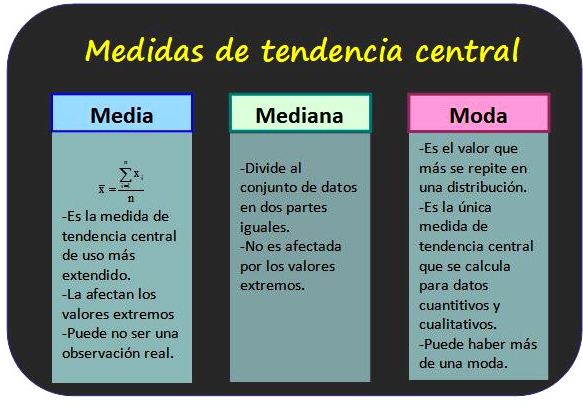
Imagen 3: Medidas de tendencia central (2022)

En esta imagen podemos ver cómo se relacionan la media, la mediana y la moda en una distribución simétrica. En una distribución simétrica, la media, la mediana y la moda son iguales.

Imagen 4: Probabilidad y Estadística Cetis21: Medidas de tendencia central

En esta imagen podemos ver cómo se calcula la mediana en un conjunto de datos que tiene valores atípicos. Podemos ver que la mediana es menos sensible a los valores extremos que la media.

Imagen 5: Mapa Conceptual De Medidas De Tendencia Central Necto Images

En esta imagen podemos ver un mapa conceptual que resume las diferencias entre la media, la mediana y la moda.

Imagen 6: Medidas estadísticas univariantes - Mind Map

En esta imagen podemos ver un mind map que muestra cómo se calculan las medidas de tendencia central.

Espero que estas imágenes te hayan ayudado a comprender mejor las medidas de tendencia central. Ahora, te daré algunos consejos para que puedas aplicar estas medidas en tu trabajo o estudio. -Conoce bien tus datos antes de elegir una medida de tendencia central. Si tus datos están sesgados o tienen valores extremos, la media puede no ser una buena elección. -Usa la mediana cuando tus datos tienen muchos valores extremos. La mediana es menos sensible a los valores atípicos que la media. -Usa la moda cuando algunos valores se repiten mucho. La moda es muy útil para encontrar patrones en los datos. Y ahora, algunas ideas para que puedas practicar el cálculo de medidas de tendencia central: -Recopila los resultados de un examen y calcula su media, mediana y moda. -Recopila los precios de un producto en diferentes tiendas y calcula su media, mediana y moda. -Recopila las alturas de tus amigos y calcula su media, mediana y moda. Finalmente, si quieres profundizar en los conocimientos sobre las medidas de tendencia central, te recomiendo que busques más información en libros o cursos de estadística. ¡Nunca es tarde para aprender! Espero que este post haya sido útil para ti. Si te gustó, compártelo con tus amigos y familiares. Y recuerda, ¡la estadística puede ser divertida!