Medidas De Tendencia Media Mediana Y Mod

¡Hola a todos! Hoy vamos a hablar sobre un tema muy importante en estadísticas: las medidas de tendencia central. Si estás estudiando estadística, es probable que ya hayas escuchado hablar de la media, la mediana y la moda. Pero, ¿sabes realmente qué son y cómo se calculan? Para entender las medidas de tendencia central, primero necesitamos revisar brevemente qué es la estadística. Se trata de una rama de las matemáticas que nos permite analizar, interpretar y presentar datos. La estadística se aplica en muchos campos, desde la economía hasta la medicina, y es fundamental para la investigación científica y el análisis de datos en el mundo actual. Ahora bien, ¿qué son las medidas de tendencia central? En resumen, se trata de herramientas que nos ayudan a resumir y describir un conjunto de datos en un solo valor. Estas medidas nos permiten conocer la posición o el centro de los datos. Por ejemplo, si queremos ver cuál es la edad promedio de las personas que asistieron a un concierto, podemos calcular la media de las edades. Veamos en detalle las tres medidas de tendencia central más comunes: Media: Se calcula sumando todos los valores de un conjunto de datos y dividiendo el resultado entre el número de datos. Es decir, es el valor que resulta de la división entre la suma del conjunto de datos y la cantidad de datos que componen ese conjunto. La media nos da una idea del valor típico de un conjunto de datos.

Calculando la media

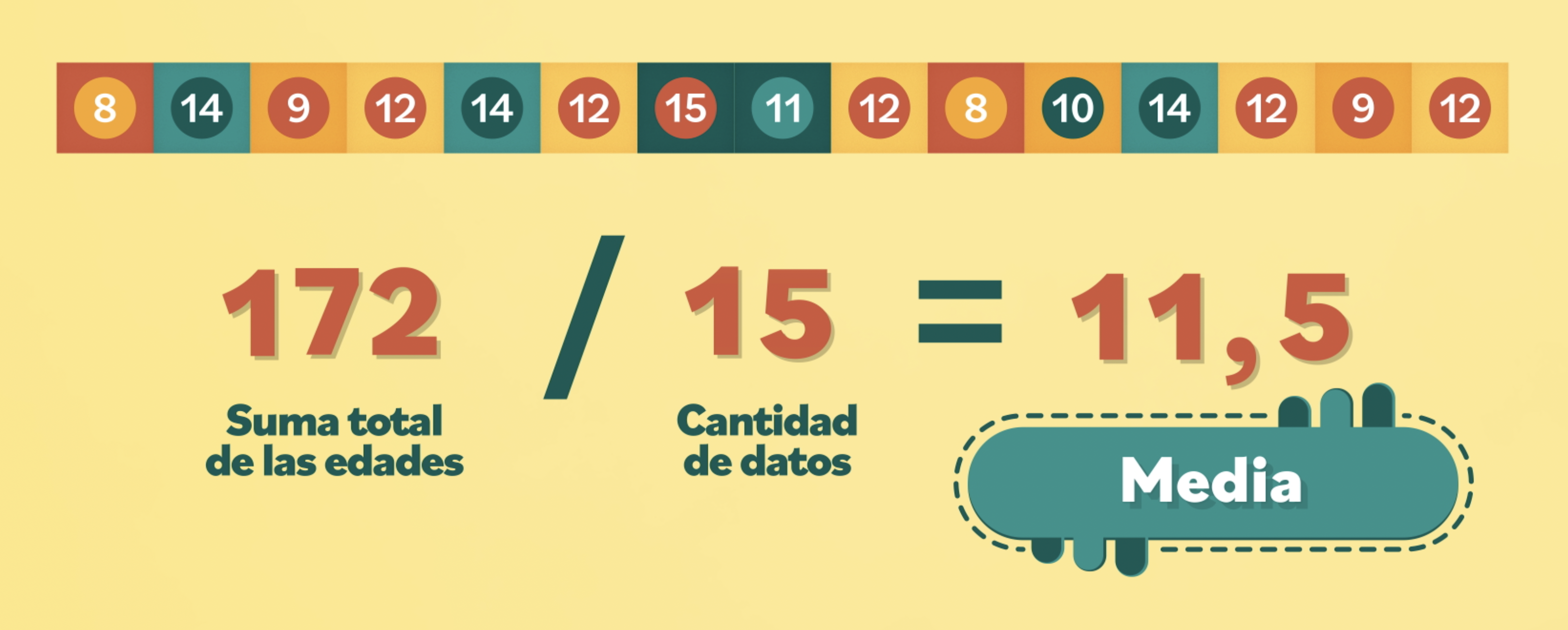
Para calcular la media, primero hay que sumar todos los valores y luego dividir el resultado entre el número de datos:

Ejemplo:

(2 + 4 + 6 + 8 + 10) ÷ 5 = 6

La media de los cinco números es 6.

Mediana: Es el valor central de un conjunto de datos ordenados. Es decir, si colocamos los datos en orden de menor a mayor, la mediana es el valor que queda justo en el centro. La mediana nos da una idea del valor central de un conjunto de datos.

Calculando la mediana

Para calcular la mediana, se ordenan los datos de menor a mayor y se busca el valor que queda en el centro:

Ejemplo:

Para encontrar la mediana de los números 2, 4, 6, 8, y 10, primero se ordenan:

2, 4, 6, 8, 10

La mediana es el número que queda justo en el centro, que en este caso es 6.

Moda: Es el valor que aparece con mayor frecuencia en un conjunto de datos. Es decir, es el valor que se repite más veces. La moda nos da una idea del valor más común o frecuente de un conjunto de datos.

Calculando la moda

Para encontrar la moda, se busca el valor que se repite con mayor frecuencia:

Ejemplo:

En el conjunto de números 2, 4, 6, 8, y 10, ningún valor se repite más de una vez, por lo que no hay moda.

En el conjunto de números 2, 5, 5, 7, y 9, el valor que se repite más veces es 5, por lo que la moda es 5.

Ahora que ya sabemos qué son y cómo se calculan cada una de estas medidas de tendencia central, es importante recordar que cada una de ellas puede tener sus ventajas y desventajas dependiendo del conjunto de datos que se esté analizando. En algunos casos, puede ser más apropiado utilizar la media, mientras que en otros la mediana o la moda pueden ser más representativas. Algunos consejos útiles para trabajar con medidas de tendencia central: - Si tienes un conjunto de datos muy grandes, es posible que la media se vea afectada por valores extremos (muy altos o muy bajos). En estos casos, puede ser más representativo utilizar la mediana. - Si tienes un conjunto de datos en el que la mayoría de valores se repiten una o pocas veces y solo unos pocos valores se repiten muchas veces, es posible que la moda sea la medida más representativa. - Es importante recordar que las medidas de tendencia central pueden variar dependiendo de la forma en que se obtengan los datos. Por ejemplo, si recopilamos datos en diferentes momentos del día, es posible que la media varíe. Por eso es importante tener en cuenta la fuente y el contexto de los datos. Ideas para practicar el cálculo de medidas de tendencia central: - Recopila datos de tus amigos o familiares (como la altura, el peso o la edad) y calcula la media, la mediana y la moda. - Busca alguna encuesta o estudio en línea y practica el cálculo de las diferentes medidas de tendencia central utilizando los datos proporcionados. - Practica el cálculo de medidas de tendencia central utilizando una calculadora o una hoja de cálculo. Como puedes ver, las medidas de tendencia central son una herramienta fundamental en estadística. Si estás estudiando esta disciplina, es importante que comprendas bien qué son y cómo se calculan. Y si no estás en el mundo de la estadística, esta información puede ser útil en diversos contextos de la vida cotidiana. ¡Espero que hayas disfrutado de este post y aprendido algo nuevo!