Definicion De Medidas De Tendencia Central Media Mediana Moda Quimica

¡Hola a todos y todas! Hoy vamos a hablar sobre un tema muy interesante en el mundo de las matemáticas: las medidas de tendencia central. Si bien puede sonar un poco aburrido, en realidad estas medidas son muy importantes y útiles para interpretar y analizar datos.

Media

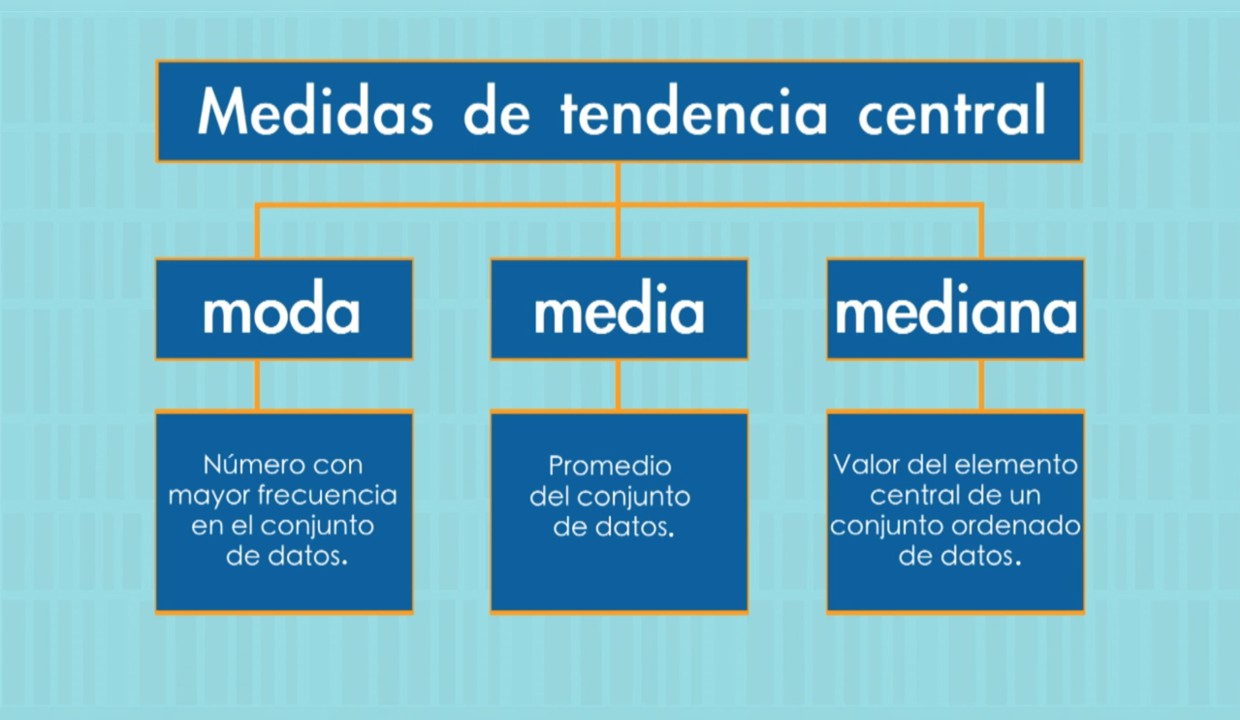
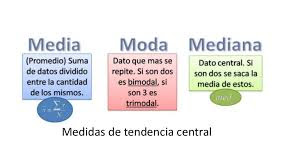
Comencemos por la media. Ésta es la medida más común utilizada para obtener la tendencia central de un conjunto de datos. Para calcularla, sumamos todos los valores y dividimos entre la cantidad de valores que tenemos. Por ejemplo, supongamos que tenemos los siguientes datos de temperaturas en grados Celsius:

• 10
• 12
• 13
• 15
• 20

Para obtener la media, sumamos todos los valores: 10 + 12 + 13 + 15 + 20 = 70. Luego dividimos entre la cantidad de valores, que en este caso es 5. Por lo tanto, la media de este conjunto de datos es 14.

Mediana

La mediana es otra medida de tendencia central que se utiliza comúnmente. Para obtenerla, debemos ordenar los datos de menor a mayor y seleccionar el valor que se encuentra en el centro de la lista. En el ejemplo anterior, los datos ya están ordenados, por lo que podemos decir que la mediana es 13.

Moda

La moda es el valor más frecuente en un conjunto de datos. En el ejemplo anterior, no hay un valor que se repita más que otro, por lo que no existe moda. Sin embargo, en otros conjuntos de datos es posible que haya más de una moda.

Consejos para interpretar las medidas de tendencia central

Ahora que ya sabemos cómo obtener la media, mediana y moda, es importante tener en cuenta algunos consejos para interpretar correctamente estas medidas:

• La media es muy sensible a los valores atípicos (outliers) en un conjunto de datos. Si tenemos valores que son muy distintos al resto, éstos pueden afectar significativamente el valor de la media.
• La mediana es una medida más robusta y no se ve afectada por los valores atípicos.
• La moda puede no ser representativa de todo el conjunto de datos, especialmente si hay varias modas.

Ideas para aplicar las medidas de tendencia central

Quizás te estés preguntando qué aplicaciones tienen estas medidas de tendencia central en el mundo real. Aquí te dejamos algunas ideas:

• En el campo de la medicina, la media se utiliza para valorar el estado nutricional de un paciente.
• En el ámbito financiero, la mediana y la moda se utilizan para analizar el sueldo de los empleados en una empresa.
• En el análisis de datos de redes sociales, la moda se utiliza para identificar los temas más populares.

Cómo calcular las medidas de tendencia central en Excel

Si necesitas calcular la media, mediana o moda de un conjunto de datos en Excel, ¡es muy fácil! Sólo tienes que seguir estos pasos:

1. Ingresa los datos en una columna de Excel.
2. Selecciona la celda donde deseas que aparezca el resultado.
3. Utiliza las siguientes fórmulas:
   • Para la media: =PROMEDIO(A1:A5)
   • Para la mediana: =MEDIANA(A1:A5)
   • Para la moda: =MODA(A1:A5)
4. Presiona Enter y ¡listo!

Esperamos que este artículo te haya resultado interesante y útil. No dudes en dejarnos tus comentarios y preguntas. ¡Hasta la próxima!

Consejos para interpretar las medidas de tendencia central

Ahora que ya sabemos cómo obtener la media, mediana y moda, es importante tener en cuenta algunos consejos para interpretar correctamente estas medidas:

• La media es muy sensible a los valores atípicos (outliers) en un conjunto de datos. Si tenemos valores que son muy distintos al resto, éstos pueden afectar significativamente el valor de la media.
• La mediana es una medida más robusta y no se ve afectada por los valores atípicos.
• La moda puede no ser representativa de todo el conjunto de datos, especialmente si hay varias modas.

Ideas para aplicar las medidas de tendencia central

Quizás te estés preguntando qué aplicaciones tienen estas medidas de tendencia central en el mundo real. Aquí te dejamos algunas ideas:

• En el campo de la medicina, la media se utiliza para valorar el estado nutricional de un paciente.
• En el ámbito financiero, la mediana y la moda se utilizan para analizar el sueldo de los empleados en una empresa.
• En el análisis de datos de redes sociales, la moda se utiliza para identificar los temas más populares.

Cómo calcular las medidas de tendencia central en Excel

Si necesitas calcular la media, mediana o moda de un conjunto de datos en Excel, ¡es muy fácil! Sólo tienes que seguir estos pasos:

1. Ingresa los datos en una columna de Excel.
2. Selecciona la celda donde deseas que aparezca el resultado.
3. Utiliza las siguientes fórmulas:
   • Para la media: =PROMEDIO(A1:A5)
   • Para la mediana: =MEDIANA(A1:A5)
   • Para la moda: =MODA(A1:A5)
4. Presiona Enter y ¡listo!

Esperamos que este artículo te haya resultado interesante y útil. No dudes en dejarnos tus comentarios y preguntas. ¡Hasta la próxima!

Consejos para interpretar las medidas de tendencia central

Ahora que ya sabemos cómo obtener la media, mediana y moda, es importante tener en cuenta algunos consejos para interpretar correctamente estas medidas:

• La media es muy sensible a los valores atípicos (outliers) en un conjunto de datos. Si tenemos valores que son muy distintos al resto, éstos pueden afectar significativamente el valor de la media.
• La mediana es una medida más robusta y no se ve afectada por los valores atípicos.
• La moda puede no ser representativa de todo el conjunto de datos, especialmente si hay varias modas.

Ideas para aplicar las medidas de tendencia central

Quizás te estés preguntando qué aplicaciones tienen estas medidas de tendencia central en el mundo real. Aquí te dejamos algunas ideas:

• En el campo de la medicina, la media se utiliza para valorar el estado nutricional de un paciente.
• En el ámbito financiero, la mediana y la moda se utilizan para analizar el sueldo de los empleados en una empresa.
• En el análisis de datos de redes sociales, la moda se utiliza para identificar los temas más populares.

Cómo calcular las medidas de tendencia central en Excel

Si necesitas calcular la media, mediana o moda de un conjunto de datos en Excel, ¡es muy fácil! Sólo tienes que seguir estos pasos:

1. Ingresa los datos en una columna de Excel.
2. Selecciona la celda donde deseas que aparezca el resultado.
3. Utiliza las siguientes fórmulas:
   • Para la media: =PROMEDIO(A1:A5)
   • Para la mediana: =MEDIANA(A1:A5)
   • Para la moda: =MODA(A1:A5)
4. Presiona Enter y ¡listo!

Esperamos que este artículo te haya resultado interesante y útil. No dudes en dejarnos tus comentarios y preguntas. ¡Hasta la próxima!

Cómo interpretar las medidas de tendencia central

En resumen, las medidas de tendencia central son una herramienta fundamental para el análisis e interpretación de los datos. La media, mediana y moda nos brindan una noción sobre el comportamiento de los datos, su tendencia y su distribución. Es importante tener en cuenta los consejos que mencionamos previamente antes de tomar decisiones o conclusiones basadas en las medidas de tendencia central.

Además, aplicar estas medidas en el mundo real puede aportarnos información valiosa y útil en distintas áreas, como la medicina, finanzas y redes sociales. Y si necesitas calcular la media, mediana o moda de un conjunto de datos, ¡Excel es la herramienta ideal!

Esperamos que haya sido de ayuda este artículo y te invitamos a que sigas explorando el maravilloso mundo de las matemáticas. ¡Hasta la próxima!