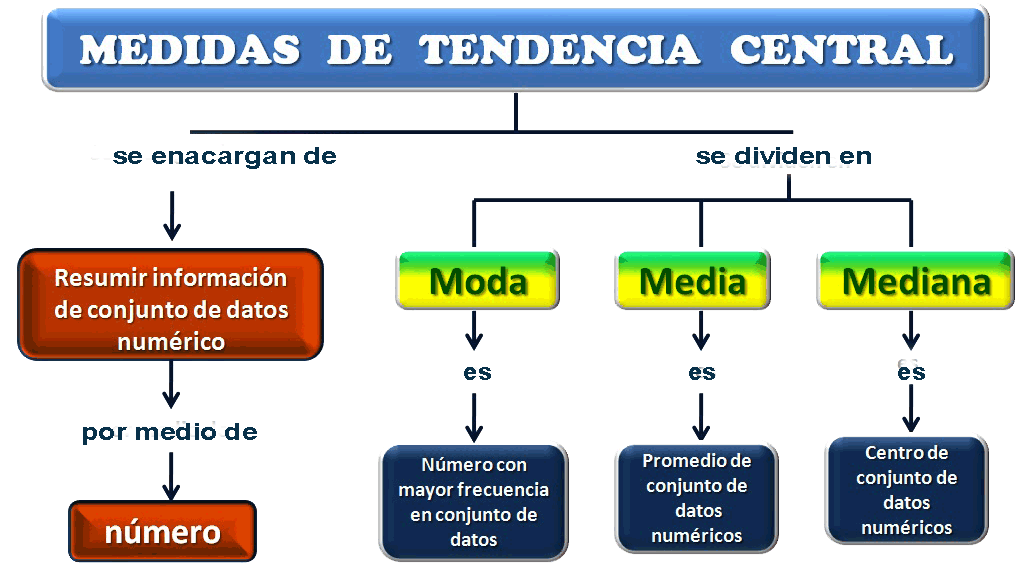
Tendencia Central Y Dispersión Moda Media Y Mediana

¡Hola, amigos! Hoy les voy a hablar sobre un tema muy importante en estadística: las medidas de tendencia central y dispersión. Este es un tema que a menudo genera confusiones y malentendidos, pero con un poco de práctica y dedicación, podrán entenderlo y aplicarlo fácilmente. Medidas de tendencia central Las medidas de tendencia central son aquellas que nos permiten conocer la posición central o típica de los datos en una muestra o población. Estas medidas son la media, la mediana y la moda.

La media

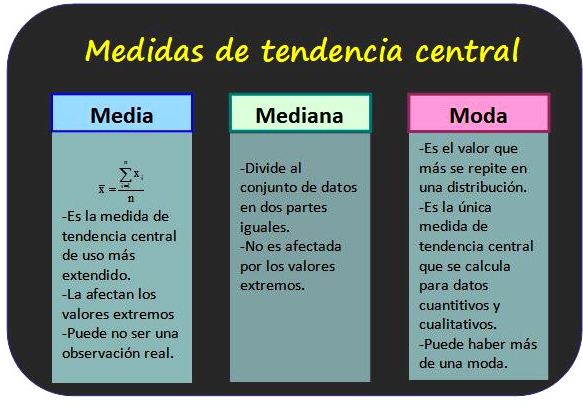
La media es el valor obtenido al sumar todos los datos y dividir el resultado entre el número de datos. Es decir, es la suma de los valores divididos entre la cantidad de valores.

Consejos:

• La media se ve afectada por los datos extremos, también conocidos como outliers. Por lo tanto, es importante considerarlos al momento de analizar la media.
• La media no siempre es un valor presente en los datos, ya que puede ser un valor decimal o incluso irracional. En estos casos, podemos redondearla a un número concreto que tenga sentido para el contexto del problema.

La mediana

La mediana es el valor central de un conjunto de datos cuando éstos se ordenan de menor a mayor o de mayor a menor. Es decir, es el valor que se encuentra en la mitad de los datos.

Ideas:

• La mediana es una medida robusta, ya que no se ve afectada por los datos extremos o atípicos.
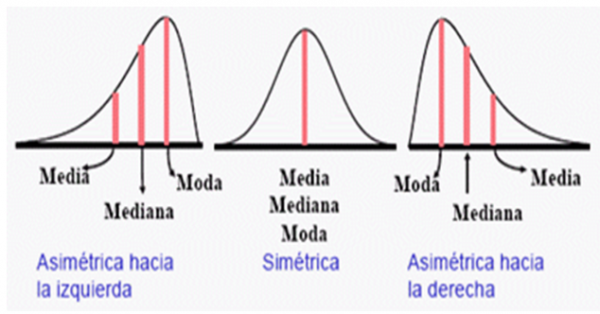
• La mediana es muy útil para datos que se distribuyen de forma asimétrica.

La moda

La moda es el valor que más se repite en un conjunto de datos. Es decir, es el valor que tiene mayor frecuencia absoluta.

Como:

• La moda puede tener limitaciones en cuanto a su uso cuando hay más de una moda, ya que no podemos representarlas todas en una sola medida.
• La moda no siempre es útil para describir conjuntos de datos continuos o en los que no hay datos repetidos.

Medidas de dispersión Las medidas de dispersión nos indican cuánto se alejan los datos de la medida de tendencia central. Las medidas de dispersión son la desviación estándar, el rango intercuartílico y el coeficiente de variación.

La desviación estándar

La desviación estándar es una medida que representa cuánto se alejan los datos de la media. Es decir, mide la dispersión de los datos respecto a la media.

Consejos:

• La desviación estándar es una medida muy sensible a los datos extremos. Por lo tanto, es importante considerarlos al momento de analizar la desviación estándar.
• La desviación estándar puede interpretarse en relación a la media. Por ejemplo, si la desviación estándar es pequeña, los datos tienden a estar cerca de la media.

El rango intercuartílico

El rango intercuartílico es una medida que representa la distancia entre el tercer y primer cuartil de un conjunto de datos. Es decir, mide el rango de valores que abarca el 50% de los datos centrales.

Ideas:

• El rango intercuartílico es una medida robusta, ya que no se ve afectada por los datos extremos o atípicos.
• El rango intercuartílico es muy aplicable en datos que se distribuyen de forma asimétrica y tienen una gran cantidad de datos extremos.

El coeficiente de variación

El coeficiente de variación es una medida que representa la relación entre la desviación estándar y la media. Es decir, mide la variabilidad relativa de los datos respecto a la media.

Como:

• El coeficiente de variación es muy útil al momento de comparar la variabilidad de dos o más conjuntos de datos que tengan escalas distintas.
• El coeficiente de variación puede no ser útil o representativo para datos en los que la media es cero o muy cercana a cero.

Espero que estos consejos les hayan sido de utilidad para entender y aplicar las medidas de tendencia central y dispersión en sus análisis estadísticos. Recuerden que la práctica y la interpretación de los datos es fundamental para su correcta aplicación. ¡Nos vemos en el próximo post!