Medidas De Tendencia Central Ejemplos Moda Mei

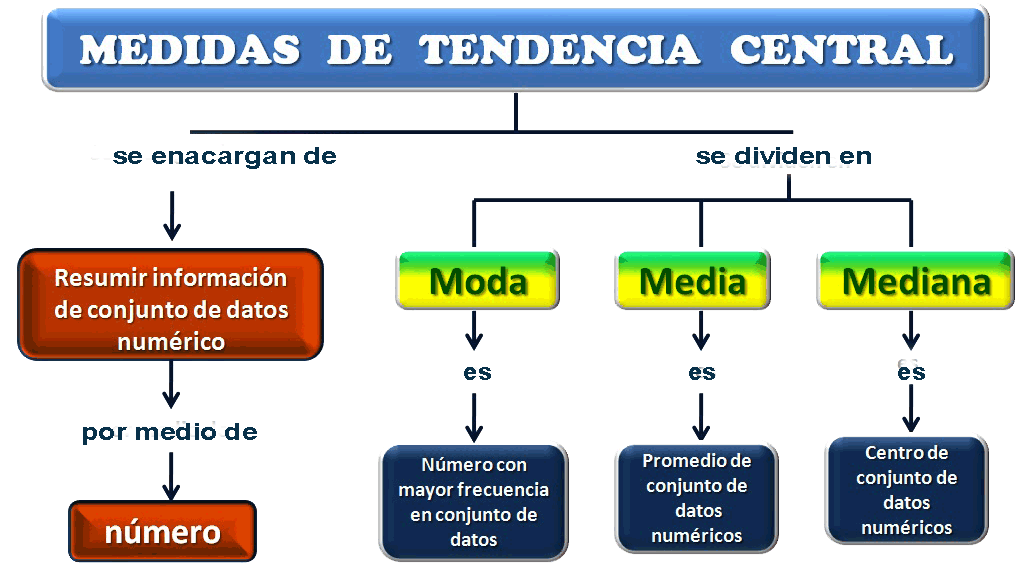
En la estadística, las medidas de tendencia central representan valores que se encuentran en el centro de un conjunto de datos. Las tres medidas de tendencia central más comunes son la media, la mediana y la moda. En este post, vamos a profundizar en estas medidas y cómo se pueden utilizar para analizar datos y tomar decisiones más informadas.

La media

La media es la medida de tendencia central más conocida y se utiliza con frecuencia para describir el "promedio" de un conjunto de datos. Se calcula sumando todos los valores del conjunto de datos y dividiéndolos por la cantidad de valores. Por ejemplo, si tenemos los siguientes valores:

• 5, 9, 3, 2, 8, 1, 6

La media sería:

(5 + 9 + 3 + 2 + 8 + 1 + 6) / 7 = 4.28

Lo que significa que, en promedio, los valores del conjunto de datos están alrededor de 4.28.

La mediana

La mediana es el valor medio de un conjunto de datos. Para calcularla, se ordenan los valores de menor a mayor y se identifica el valor que se encuentra en el centro del conjunto de datos. Si hay un número par de valores, se calcula el promedio de los dos valores centrales. Por ejemplo, con los siguientes valores:

• 5, 9, 3, 2, 8, 1, 6

La mediana sería 5, ya que es el valor central en el conjunto de datos ordenado.

La moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Si un conjunto de datos tiene dos o más valores que aparecen con la misma frecuencia máxima, entonces el conjunto de datos tiene más de una moda. Por ejemplo, con los siguientes valores:

• 5, 9, 3, 2, 8, 1, 6, 5

La moda sería 5, ya que es el valor que aparece con mayor frecuencia en el conjunto de datos.

Consejos para interpretar las medidas de tendencia central

Es importante tener en cuenta que las medidas de tendencia central por sí solas no proporcionan información completa sobre un conjunto de datos. Es importante considerar otras medidas estadísticas, como la desviación estándar, la varianza y el rango intercuartílico. Además, es importante considerar el contexto de los datos y las posibles causas detrás de las tendencias observadas.

Ideas para utilizar las medidas de tendencia central

Hay muchas formas en que las medidas de tendencia central se pueden utilizar en situaciones cotidianas. Por ejemplo, los gerentes pueden utilizar la media para analizar los registros de ventas mensuales y determinar el promedio de ventas en un período de tiempo determinado. Los representantes de recursos humanos también pueden utilizar la moda para determinar la edad más común de los empleados en un determinado departamento o compañía.

Cómo calcular las medidas de tendencia central

Hay muchas herramientas disponibles en línea que pueden ayudar a calcular la media, la mediana y la moda. Las hojas de cálculo de Excel también tienen fórmulas integradas para calcular estas medidas. Es importante tener en cuenta que diferentes conjuntos de datos pueden requerir diferentes enfoques para calcular las medidas de tendencia central, y que el contexto de los datos es crucial para su interpretación adecuada.

Conclusión

En resumen, las medidas de tendencia central son una forma útil de resumir los datos y pueden proporcionar información valiosa en una variedad de situaciones. Sin embargo, también es importante considerar otras medidas estadísticas y el contexto de los datos para una interpretación adecuada. Con un conocimiento sólido de las medidas de tendencia central y cómo calcularlas, se puede tomar decisiones más informadas en una amplia variedad de contextos.

Consejos para interpretar las medidas de tendencia central

Cuando se interpreta la media, hay que tener en cuenta que esta medida puede ser influenciada por valores extremos, lo que conocemos como valores atípicos. Si existen valores extremos en un conjunto de datos, puede ser conveniente utilizar la mediana en lugar de la media para describir el conjunto de datos.

Ideas para utilizar las medidas de tendencia central

Si se está trabajando con un conjunto de datos con una distribución normal, la media, la mediana y la moda serán iguales. En estos casos, la media es una medida adecuada de tendencia central que proporciona una descripción precisa de los datos.

Cómo calcular las medidas de tendencia central

Como hemos mencionado, Excel cuenta con fórmulas para calcular la media, la mediana y la moda. Además, existen herramientas en línea como calculadoras de estadísticas y programación de software estadístico, como R y Python, que ofrecen soluciones más avanzadas para el análisis de datos.

Conclusión

Las medidas de tendencia central son herramientas útiles para resumir datos y proporcionar información valiosa en una amplia variedad de contextos. Con un conocimiento sólido de la media, la mediana y la moda, se puede tomar decisiones más informadas y comprender mejor los datos que se presentan en situaciones cotidianas y profesionales.

Consejos para interpretar las medidas de tendencia central

Cuando se trabaja con diferentes conjuntos de datos, es importante considerar la naturaleza de los datos, si son discretos o continuos, y seleccionar la medida de tendencia central adecuada. Por ejemplo, si está trabajando con datos continuos, la media puede ser una mejor descripción que la moda, mientras que si está trabajando con datos discretos, la moda puede ser la medida de tendencia central más adecuada.

Ideas para utilizar las medidas de tendencia central

Un gerente de recursos humanos puede utilizar la mediana para analizar los salarios de los empleados en su compañía y determinar la mediana para establecer un salario base. Los científicos de investigación pueden utilizar la media para analizar los datos de los experimentos y encontrar patrones en los datos.

Cómo calcular las medidas de tendencia central

Las medidas de tendencia central son fáciles de calcular con una calculadora y algo de tiempo para ordenar y manipular los datos. Además, también existen herramientas y software especializado para realizar análisis estadísticos más complejos.