Ejemplos De Las Medidas De Tendencia Central Moda

En la estadística, existen diferentes maneras de medir el centro de un conjunto de datos, estas medidas se conocen como medidas de tendencia central. En este artículo, exploraremos las ventajas y desventajas de la media, mediana y moda estadística, y cómo estas medidas pueden ayudarnos a comprender mejor los datos.

Media

La media es la medida de tendencia central más familiar. Es la suma de todos los datos dividido por el número de datos. Por lo tanto, es una medida sensible a todos los valores en el conjunto de datos.

Consejos:

• La media puede ser influenciada por valores extremos (outliers) en el conjunto de datos. Por lo tanto, es importante considerar la presencia de valores atípicos antes de utilizar la media como medida de tendencia central.
• La media puede no ser representativa de la distribución de datos si hay una cantidad significativa de valores extremos o si la distribución es asimétrica.

Ideas:

• La media es útil para resumir datos y encontrar un promedio. Por ejemplo, el salario promedio de los empleados de una empresa.
• La media es utilizada en muchas pruebas estadísticas, como las pruebas t de Student.

Como:

Para calcular la media, se suman todos los valores en el conjunto de datos y se dividen por el número total de valores. La fórmula matemática es:

media = (suma de todos los valores) / (número total de valores)

Mediana

La mediana es el valor central en un conjunto de datos, cuando los datos están ordenados de menor a mayor. Si el número de datos es impar, la mediana es el valor en la mitad del conjunto. Si el número de datos es par, la mediana es el promedio de los dos valores centrales. La mediana puede ser una mejor medida de tendencia central que la media si hay valores extremos en el conjunto de datos.

Consejos:

• La mediana no es sensible a los valores extremos en el conjunto de datos.
• La mediana puede no ser representativa de la distribución de datos si hay valores atípicos en el conjunto de datos.
• La mediana puede ser más difícil de calcular si el conjunto de datos es grande o si los datos tienen muchos valores repetidos.

Ideas:

• La mediana es útil para describir la distribución de datos cuando hay valores extremos en el conjunto de datos.
• La mediana es útil para resumir datos que no tienen una distribución normal.

Como:

Para calcular la mediana, se ordenan los valores en el conjunto de datos de menor a mayor y se encuentra el valor central. Si hay un número impar de datos, el valor central es la mediana. Si hay un número par de datos, se encuentra el promedio de los dos valores centrales.

Moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Si no hay un valor que aparezca con mayor frecuencia, entonces no hay moda en el conjunto de datos. La moda es útil para resumir la distribución de datos, y puede ser una medida de tendencia central útil en conjuntos de datos con valores repetidos.

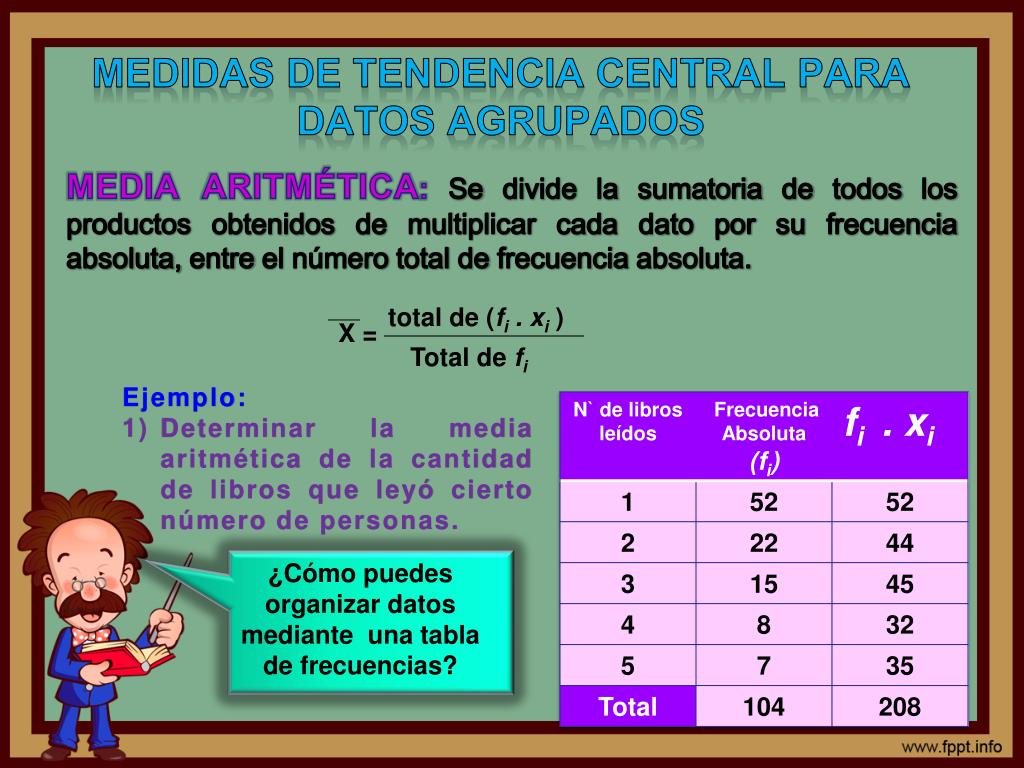
Consejos:

• La moda sólo es una medida de tendencia central cuando hay valores repetidos en el conjunto de datos.
• La moda puede no ser representativa de la distribución de datos si la distribución es bimodal o multimodal.

Ideas:

• La moda es útil para resumir datos que tienen una distribución de datos con valores repetidos.
• La moda es útil para identificar valores que son importantes para el conjunto de datos.

Como:

Para encontrar la moda, se encuentra el valor que aparece con mayor frecuencia en el conjunto de datos. Si no hay un valor que aparezca con mayor frecuencia, entonces no hay moda.

Conclusiones

La elección de la medida de tendencia central adecuada depende de la distribución de los datos y del objetivo del análisis de datos. Si los datos tienen una distribución normal y no hay valores extremos significativos, la media puede ser una medida de tendencia central útil. Si los datos tienen valores extremos o no tienen una distribución normal, la mediana puede ser una mejor medida de tendencia central. Si los datos tienen valores repetidos, la moda puede ser una medida de tendencia central útil.

En definitiva, las medidas de tendencia central son herramientas útiles que nos ayudan a comprender mejor los datos y resumirlos para su análisis. Es importante tener en cuenta las ventajas y desventajas de cada medida de tendencia central antes de decidir cuál utilizar en un análisis de datos.