¡Qué tal, mi gente! Hoy nos vamos a adentrar en el mundo de la estadística y las medidas de tendencia central. ¿Por qué es algo importante para nosotros? Pues porque si queremos entender y mejorar nuestra vida económica, social y personal, necesitamos saber cómo se miden los datos y analizarlos en función de la media, la moda y la mediana. Empecemos por la definición. La media, es el valor obtenido al sumar todos los datos y dividirlos por el número total de datos. La moda, es el valor que aparece con mayor frecuencia en una serie de datos. La mediana, es el valor que se encuentra en el centro de una serie de datos ordenados de menor a mayor. Ahora, veamos cómo aplicamos estas medidas en la vida real. Imagínense que queremos saber cuánto nos gastamos al mes en el supermercado. Tomamos los datos de cada compra y los sumamos. Dividimos la suma entre el número total de compras realizadas y tenemos la media. Si, por ejemplo, nuestra media de gastos en el supermercado es de $100, podemos evaluar si estamos gastando demasiado o si debemos ajustar nuestro presupuesto. Otro ejemplo común es el uso de estas medidas en la salud. Si evaluamos el índice de masa corporal (IMC) de cada persona, podemos obtener la media de ese grupo. Si alguien tiene un IMC fuera de la media, podemos analizar su situación y ofrecerle consejos o soluciones para mejorar su salud. Ahora, vamos a ver algunos ejemplos prácticos a través de imágenes.
Imagen 1: ESTADISTICA Y MEDIDA DE TENDENCIA CENTRAL
En esta imagen podemos ver una tabla que muestra los valores de la media, moda y mediana de una serie de datos. En este caso, la media es 6, la moda es 2 y la mediana es 3. Esto nos indica que tenemos una serie de datos con una distribución asimétrica, es decir, que hay valores que se repiten menos que otros. Consejo: Si tienes una serie de datos con una distribución asimétrica, es importante considerar la mediana como una medida de tendencia central, ya que no se ve afectada por los valores extremos.
Imagen 2: Medidas de tendencia central
En esta imagen podemos ver una representación gráfica de los datos para visualizar cómo se distribuyen. Podemos ver claramente que la moda es 18, ya que es el valor que más se repite. La mediana, en cambio, es 15, que es el valor central entre los datos ordenados en forma ascendente. Consejo: La moda es especialmente útil cuando necesitas identificar valores atípicos, ya que te ayuda a identificar los valores que aparecen con mayor frecuencia.
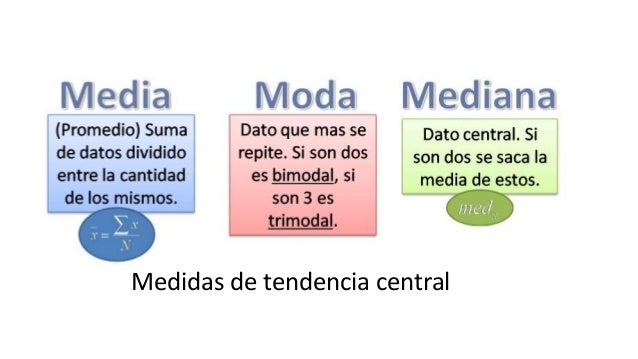
Imagen 3: Media, Moda Y Mediana Super Facil, Medidas De Tendencia Central
En esta imagen podemos ver un tutorial en video para aprender a calcular la media, moda y mediana de una serie de datos. Aunque es importante conocer cómo se calculan estas medidas, también podemos utilizar programas de ordenador que lo hagan por nosotros. Ideas: Si eres estudiante, es útil conocer cómo se calculan estas medidas para poder realizar investigaciones y análisis de datos. Si eres profesional, es recomendable utilizar programas de ordenador que faciliten el proceso y proporcionen gráficos y visualizaciones para un mejor análisis.
Imagen 4: Medidas De Tendencia Central Media Mediana Y Moda Youtube – ThemeLower
En esta imagen podemos ver otro tutorial en video para aprender a calcular la media, mediana y moda. Este tutorial utiliza ejemplos prácticos de la vida diaria para explicar las medidas de tendencia central. Como: Si tienes problemas para entender cómo se calculan estas medidas, te recomendamos buscar tutoriales en línea y videos explicativos que te puedan ayudar a comprender mejor.
Imagen 5: MEDIDAS DE TENDENCIA CENTRAL ESTADISTICA EJERCICIOS RESUELTOS PDF
En esta imagen podemos ver un ejemplo de ejercicios resueltos de medidas de tendencia central. Es importante practicar con ejercicios similar para familiarizarse con el proceso de cálculo y mejorar la comprensión. Consejo: Utiliza ejercicios similares para practicar el cálculo de las medidas de tendencia central y mejorar la precisión en los resultados.
Imagen 6: SEXTO GRADO GRUPO "B": MEDIDAS DE TENDENCIA...MATEMÁTICAS TERCER
En esta imagen podemos ver una infografía que nos explica de manera visual las medidas de tendencia central. La imagen muestra cómo se obtiene la media, moda, mediana y cómo se calcula en función de los datos obtenidos. Como: Si eres un estudiante, te recomendamos buscar infografías y resúmenes visuales para ayudar a tu comprensión de las medidas de tendencia central. ¡Eso es todo por hoy, mi gente! Espero que esta breve introducción a las medidas de tendencia central les haya sido útil para comprender su importancia y cómo se aplican en la vida diaria. Recuerden que, aunque pueda parecer complicado, con la práctica y la paciencia se pueden lograr grandes avances. ¡Hasta la próxima!
Publicar un comentario for "Media Moda Super Facil Medida De Tendencia Central"