Ejemplos De Moda Medidas De Tendencia Central

¡Hola amigos! Hoy hablaremos sobre las medidas de tendencia central. ¿Alguna vez te has preguntado cuál es el valor central de un conjunto de datos? Las medidas de tendencia central son una forma de responder a esta pregunta y nos facilitan el análisis estadístico de un conjunto de datos. A continuación, les mostraré algunas imágenes y explicaré las medidas de tendencia central que se pueden utilizar.

Medidas de tendencia central

La media, la mediana y la moda son las medidas de tendencia central más utilizadas en el análisis estadístico. Cada una de estas medidas representa un valor central en un conjunto de datos, pero se calculan de manera diferente:

La media es el valor promedio de un conjunto de datos. Se calcula sumando todos los valores del conjunto y dividiendo el resultado entre el número total de valores.

La mediana es el valor central en una lista ordenada de valores. Si el conjunto de datos tiene una cantidad par de valores, se promedian los dos valores centrales.

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Puede haber una o varias modas en un conjunto de datos.

Índices estadísticos de variables cuantitativas

Existe una variedad de índices estadísticos que se pueden utilizar para analizar variables cuantitativas. Los más comunes son la media, la desviación estándar, el coeficiente de variación y la correlación. Cada uno de estos índices nos permite analizar diferentes aspectos de un conjunto de datos:

La media nos muestra el valor promedio del conjunto de datos.

La desviación estándar nos indica la variabilidad de los datos en relación con la media.

El coeficiente de variación es una medida de la variabilidad relativa de los datos en relación con la media.

La correlación nos muestra si existe una relación entre dos variables cuantitativas.

Unidad estadística y ejemplos

La unidad estadística es la entidad que se utiliza para medir un conjunto de datos. La unidad estadística puede ser un individuo, una empresa, una industria o cualquier otro objeto que se esté estudiando. A continuación, les mostraré algunos ejemplos de cómo se pueden aplicar las medidas de tendencia central:

Ejemplo 1: La altura de los estudiantes de una universidad.

Para encontrar la media, se suman todas las alturas de los estudiantes y se dividen por el número total de estudiantes. La mediana sería la altura del estudiante que se encuentra en el centro cuando se ordenan las alturas de menor a mayor. La moda se encontraría contando cuántas veces aparece cada altura y viendo cuál de ellas aparece con mayor frecuencia.

Ejemplo 2: Las ventas de una tienda de ropa en un año.

Para encontrar la media, se suman todas las ventas del año y se dividen por el número total de días en que se vendió algo. La mediana sería la venta que se encuentra en el centro de la lista de ventas ordenada de menor a mayor. La moda sería la venta que se hizo más veces en el año.

Consejos para el análisis estadístico

Para realizar un análisis estadístico efectivo es importante tener en cuenta algunos consejos:

1. Seleccionar la muestra adecuada. Una muestra representativa del universo de estudio es indispensable para obtener resultados confiables.

2. Limpiar los datos. Antes de analizar los datos, hay que verificar si hay errores o valores atípicos que pueden influir negativamente en los resultados.

3. Seleccionar la medida de tendencia central adecuada. La media, la mediana y la moda son medidas de tendencia central útiles, pero hay que seleccionar la que más se adapte al tipo de datos que se está analizando.

4. Utilizar más de una medida de tendencia central. Es aconsejable utilizar más de una medida de tendencia central para tener un panorama más completo de los datos, en especial si hay valores atípicos.

5. Interpretar los resultados. Los resultados del análisis estadístico deben interpretarse a la luz de la pregunta que se está tratando de responder y del contexto en el que se recopilaron los datos.

Ideas para el uso de las medidas de tendencia central

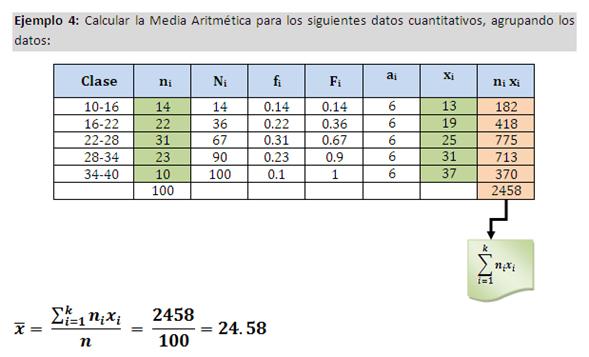
Las medidas de tendencia central son herramientas útiles para analizar una amplia variedad de datos. A continuación, les daré algunas ideas para el uso de estas medidas en diferentes ámbitos:

1. En la industria. Las medidas de tendencia central se pueden utilizar para analizar la producción, los costos y los ingresos de las empresas. Con estas medidas se pueden identificar los picos de producción, los elementos más costosos en el proceso y las tendencias de los ingresos y los costos.

2. En la salud. Las medidas de tendencia central se utilizan en la investigación médica para analizar la frecuencia de las enfermedades, la efectividad de los tratamientos y la relación entre diferentes variables.

3. En la educación. Las medidas de tendencia central se utilizan para analizar el rendimiento de los estudiantes, la efectividad de los programas educativos y la relación entre diferentes variables.

Cómo interpretar las medidas de tendencia central

Las medidas de tendencia central deben interpretarse a la luz de la pregunta que se está tratando de responder y del contexto en el que se recopilaron los datos. A continuación, les mostraré cómo interpretar cada una de las medidas de tendencia central:

1. Media. Si la media es alta, se puede concluir que el conjunto de datos tiene valores altos. Si la media es baja, se puede concluir que el conjunto de datos tiene valores bajos.

2. Mediana. Si la mediana es alta, significa que al menos la mitad de los valores del conjunto de datos están por encima de ese valor. Si la mediana es baja, significa que al menos la mitad de los valores del conjunto de datos están por debajo de ese valor.

3. Moda. Si hay una moda en el conjunto de datos, significa que hay un valor que aparece con mayor frecuencia en el conjunto de datos. Esto puede indicar que hay valores similares en el conjunto de datos.

Espero que esta información les haya sido útil para comprender las medidas de tendencia central. Recuerda que para realizar un análisis estadístico efectivo es importante tener en cuenta el contexto en el que se recopilaron los datos y seleccionar la medida de tendencia central adecuada.