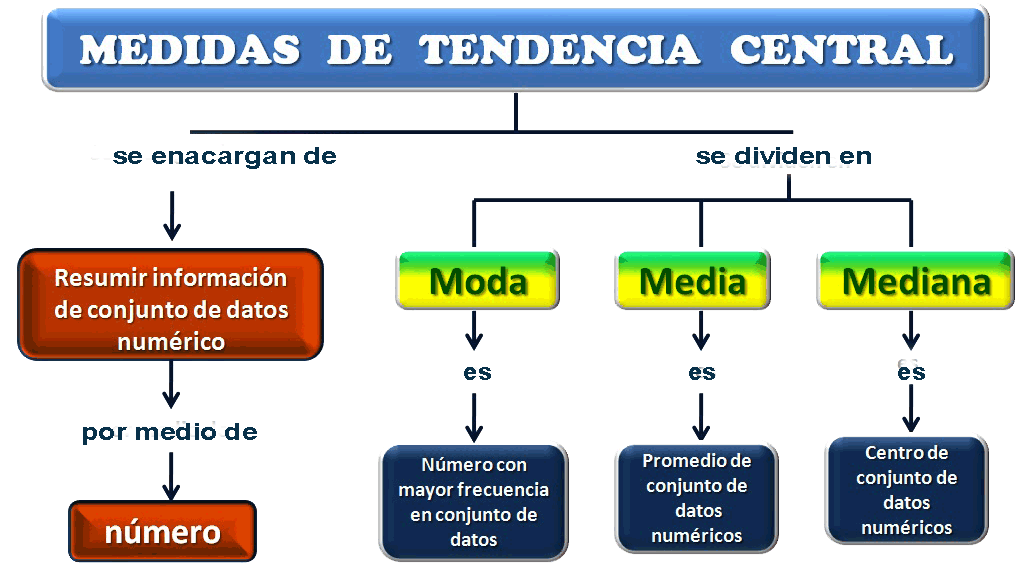
Medidas De Tendencia Central Media Moda Mediana

¡Hola, amig@s divertid@s! ¿Cómo están hoy? Espero que estén muy bien, llenos de energía y listos para aprender algo nuevo. Porque hoy hablaremos de las medidas de tendencia central, ¡y les prometo que será tan divertido como contar chistes! Pero primero, ¿qué son las medidas de tendencia central? Básicamente, son cifras que nos permiten conocer el valor central en un conjunto de datos. Así, podemos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos. Ahora, no se preocupen si esto suena complicado, ¡porque lo vamos a explicar paso a paso! Primero, empecemos con la media. La media es simplemente el promedio de todos los datos de un conjunto. Es decir, si tenemos un conjunto de números, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos. Por ejemplo, imagina que tenemos los siguientes números: 2, 4, 6, 8 y 10. Para encontrar la media, simplemente sumamos estos números: 2 + 4 + 6 + 8 + 10 = 30. Luego, dividimos este resultado entre la cantidad de números que tenemos, en este caso 5: 30 ÷ 5 = 6. Por lo tanto, la media de este conjunto de datos es 6. ¡Pero espera, hay más! La mediana es otro tipo de medida de tendencia central que nos da el número que divide un conjunto de datos en dos partes iguales. Es decir, cuando tenemos un conjunto de datos ordenados de manera ascendente o descendente, la mediana es simplemente el número que está justo en el medio. Por ejemplo, volvamos a tomar el conjunto de datos anterior: 2, 4, 6, 8 y 10. Para encontrar la mediana, simplemente ordenamos estos números de menor a mayor: 2, 4, 6, 8 y 10. Luego, buscamos el número que está en el medio, en este caso 6. Por lo tanto, la mediana de este conjunto de datos es 6. Pero, ¿y si tenemos un conjunto de datos con una cantidad impar de números? En ese caso, simplemente tomamos el número que está justo en medio, sin importar si hay otro número que lo sigue o no. Por ejemplo, imagina que tenemos los números: 1, 3, 5, 7 y 9. Para encontrar la mediana, simplemente ordenamos los números: 1, 3, 5, 7 y 9. Luego, buscamos el número que está en medio, en este caso 5. Por lo tanto, la mediana de este conjunto de datos es 5. ¡Pero todavía falta una medida de tendencia central más! La moda es simplemente el número o valor que se repite con más frecuencia en un conjunto de datos. Por ejemplo, tomemos el conjunto de datos siguiente: 2, 4, 4, 6, 8 y 10. En este caso, el número que se repite con más frecuencia es 4, por lo tanto, la moda de este conjunto de datos es 4. Ahora que ya conocen todas las medidas de tendencia central, ¡es hora de ponerlas en práctica! A continuación, les dejamos algunas imágenes que les ayudarán a entender mejor estas medidas. No se olviden de leer las consejos, ideas y como para tener una idea más amplia de su aplicación. ¡Disfruten!

Conjunto de datos: 2, 4, 6, 8, 10

Aquí tenemos un conjunto de datos con 5 números. Vamos a encontrar la media, la mediana y la moda:

La media de este conjunto de datos es 6, la mediana es 6 y la moda es 0, ya que no hay números que se repitan con más frecuencia que los demás.

Consejos:

• Recuerda que para encontrar la media, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos.
• Para encontrar la mediana, ordenamos los números de menor a mayor y buscamos el número que está en el medio.
• La moda es simplemente el número que se repite con más frecuencia en un conjunto de datos.

Ideas:

• Los números pueden representar cualquier cosa, desde las edades de un grupo de personas hasta los pesos de un paquete de dulces.
• Las medidas de tendencia central son útiles cuando queremos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos.

Cómo:

• Busca un conjunto de datos y aplica las medidas de tendencia central para encontrar la media, la mediana y la moda.
• Compara los resultados obtenidos y analiza qué medida de tendencia central te da la información más útil.

Conjunto de datos: 1, 3, 5, 7, 9

Aquí tenemos un conjunto de datos con 5 números. Vamos a encontrar la media, la mediana y la moda:

La media de este conjunto de datos es 5, la mediana es 5 y la moda es 0, ya que no hay números que se repitan con más frecuencia que los demás.

Consejos:

• Recuerda que para encontrar la media, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos.
• Para encontrar la mediana, ordenamos los números de menor a mayor y buscamos el número que está en el medio.
• La moda es simplemente el número que se repite con más frecuencia en un conjunto de datos.

Ideas:

• Los números pueden representar cualquier cosa, desde las edades de un grupo de personas hasta los pesos de un paquete de dulces.
• Las medidas de tendencia central son útiles cuando queremos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos.

Cómo:

• Busca un conjunto de datos y aplica las medidas de tendencia central para encontrar la media, la mediana y la moda.
• Compara los resultados obtenidos y analiza qué medida de tendencia central te da la información más útil.

Conjunto de datos: 4, 6, 4, 8, 10

Aquí tenemos un conjunto de datos con 5 números. Vamos a encontrar la media, la mediana y la moda:

La media de este conjunto de datos es 6, la mediana es 6 y la moda es 4, ya que el número 4 se repite con más frecuencia que los demás.

Consejos:

• Recuerda que para encontrar la media, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos.
• Para encontrar la mediana, ordenamos los números de menor a mayor y buscamos el número que está en el medio.
• La moda es simplemente el número que se repite con más frecuencia en un conjunto de datos.

Ideas:

• Los números pueden representar cualquier cosa, desde las edades de un grupo de personas hasta los pesos de un paquete de dulces.
• Las medidas de tendencia central son útiles cuando queremos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos.

Cómo:

• Busca un conjunto de datos y aplica las medidas de tendencia central para encontrar la media, la mediana y la moda.
• Compara los resultados obtenidos y analiza qué medida de tendencia central te da la información más útil.

Conjunto de datos: 1, 2, 3, 4, 4, 4, 5, 6, 7, 8, 9, 10

Aquí tenemos un conjunto de datos con 12 números. Vamos a encontrar la media, la mediana y la moda:

La media de este conjunto de datos es 5,5, la mediana es 4 y la moda es 4, ya que el número 4 se repite con más frecuencia que los demás.

Consejos:

• Recuerda que para encontrar la media, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos.
• Para encontrar la mediana, ordenamos los números de menor a mayor y buscamos el número que está en el medio.
• La moda es simplemente el número que se repite con más frecuencia en un conjunto de datos.

Ideas:

• Los números pueden representar cualquier cosa, desde las edades de un grupo de personas hasta los pesos de un paquete de dulces.
• Las medidas de tendencia central son útiles cuando queremos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos.

Cómo:

• Busca un conjunto de datos y aplica las medidas de tendencia central para encontrar la media, la mediana y la moda.
• Compara los resultados obtenidos y analiza qué medida de tendencia central te da la información más útil.

Conjunto de datos: 2, 4, 6, 8, 10, 12

Aquí tenemos un conjunto de datos con 6 números. Vamos a encontrar la media, la mediana y la moda:

La media de este conjunto de datos es 7, la mediana es 7 y la moda es 0, ya que no hay números que se repitan con más frecuencia que los demás.

Consejos:

• Recuerda que para encontrar la media, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos.
• Para encontrar la mediana, ordenamos los números de menor a mayor y buscamos el número que está en el medio.
• La moda es simplemente el número que se repite con más frecuencia en un conjunto de datos.

Ideas:

• Los números pueden representar cualquier cosa, desde las edades de un grupo de personas hasta los pesos de un paquete de dulces.
• Las medidas de tendencia central son útiles cuando queremos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos.

Cómo:

• Busca un conjunto de datos y aplica las medidas de tendencia central para encontrar la media, la mediana y la moda.
• Compara los resultados obtenidos y analiza qué medida de tendencia central te da la información más útil.

Conjunto de datos: 5, 7, 7, 10, 12, 15, 17, 19, 19, 20, 22

Aquí tenemos un conjunto de datos con 11 números. Vamos a encontrar la media, la mediana y la moda:

La media de este conjunto de datos es 13, la mediana es 15 y la moda es 7 y 19, ya que ambos números se repiten con la misma frecuencia.

Consejos:

• Recuerda que para encontrar la media, simplemente sumamos todos los números y luego los dividimos entre la cantidad de números que tenemos.
• Para encontrar la mediana, ordenamos los números de menor a mayor y buscamos el número que está en el medio.
• La moda es simplemente el número que se repite con más frecuencia en un conjunto de datos.

Ideas:

• Los números pueden representar cualquier cosa, desde las edades de un grupo de personas hasta los pesos de un paquete de dulces.
• Las medidas de tendencia central son útiles cuando queremos tener una idea de cuál es el valor que, en promedio, se repite con mayor frecuencia en un grupo de datos.

Cómo:

• Busca un conjunto de datos y aplica las medidas de tendencia central para encontrar la media, la mediana y la moda.
• Compara los resultados obtenidos y analiza qué medida de tendencia central te da la información más útil.

Esperamos que estas imágenes y consejos les hayan sido de ayuda para entender mejor las medidas de tendencia central. Recuerden que estas medidas pueden ser muy útiles en todo tipo de investigación y análisis de datos. Así que la próxima vez que se enfrenten a un conjunto de datos, ¡no tengan miedo de utilizar estas medidas para sacar lo mejor de ellos! Y sobre todo, ¡diviértanse aprendiendo!